Odchylenie standardowe w pracy magisterskiej. Jak je obliczyć?

Ostatnia aktualizacja 17 września 2025

Odchylenie standardowe w pracy magisterskiej? Teraz pewnie zapytasz, po co mi to potrzebne? Pozwól, że wyjaśnię Ci na przykładzie.

Wyobraź sobie dwie grupy studentów. W obu średnia ocena = 4,0. Brzmi identycznie? A jednak w pierwszej każdy ma 4. W drugiej są dwójki, trójki, piątki i szóstki. Ta sama średnia, zupełnie inny klimat.
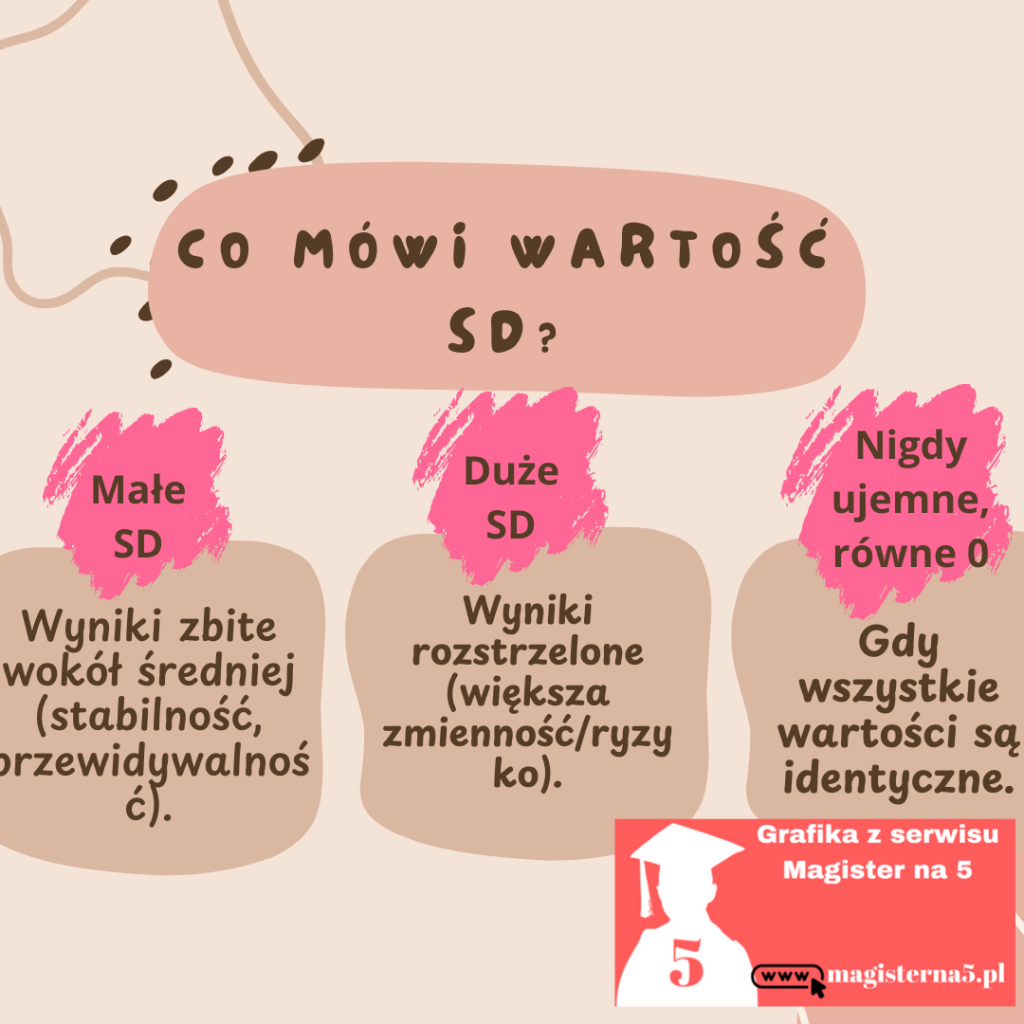
I tu wchodzi odchylenie standardowe (SD) – miara, która pokazuje, jak bardzo wyniki rozjeżdżają się wokół średniej. Małe SD = wszyscy trzymają podobny poziom. Duże SD = rollercoaster.

W tym artykule w prosty sposób wyjaśnię, czym jest odchylenie standardowe w pracy licencjackiej i magisterskiej, pokażę jak je obliczyć krok po kroku, zrobimy to też w Excelu, a na końcu dowiesz się, jak mądrze wykorzystać SD w pracy dyplomowej. Zero żargonu, dużo przykładów. Gotów? Jedziemy.

Potrzebujesz szybkiej pomocy z obliczeniem mediany w swojej pracy dyplomowej? Kliknij poniżej
–> Odchylenie standardowe w pracy magisterskiej. Błyskawiczna pomoc
–> Wzory rozdziałów badawczych ze statystyką

Nie wiem, jak zacząć. Masz coś dla mnie?
–> E-book- Jak Napisać Pracę Dyplomową W Tydzień
–> Pobierz przykładową pracę licencjacką

Czym jest odchylenie standardowe w pracy licencjackiej i magisterskiej?

Najprościej:

odchylenie standardowe to przeciętna odległość wyników od średniej.

Wyobraź sobie chmurkę punktów wokół średniej: jeśli wszystkie wyniki kleją się blisko niej, chmurka jest zwarta i SD jest małe; jeśli dane latają po całej osi, chmurka się rozlewa i SD rośnie. To właśnie sedno hasła „odchylenie standardowe”.

W zapisie spotkasz dwa symbole:

σ (sigma) dla populacji i s dla próby.

W pracach dyplomowych najczęściej korzystasz z s (bo badanie to próba, nie cała populacja). Jednostki SD są takie same jak Twoje dane: minuty dla czasu, złote dla wydatków, punkty dla ocen. Dzięki temu możesz od razu zrozumieć skalę: „SD = 6 min” mówi intuicyjnie, jak mocno rozstrzelone są czasy dojazdu.

Żeby złapać intuicję, pomyśl o dwóch grupach z tą samą średnią 4,0. W pierwszej każdy ma 4 — odchylenie standardowe ≈ 0 (wszyscy tacy sami). W drugiej są dwójki, trójki, piątki i szóstki — SD jest duże, bo wyniki odstają od średniej w obie strony. W języku statystyki mówimy wtedy, że zmienność jest wysoka. Dwie praktyczne zasady:

SD nigdy nie jest ujemne i wynosi 0 tylko wtedy, gdy wszystkie wartości są identyczne.

A więc: małe SD = wyniki są zbite i przewidywalne; duże SD = wyniki są rozstrzelone i zaskakujące. Zaraz pokażę Ci, skąd to SD się bierze „pod maską” i jak je policzyć krok po kroku — najpierw na kartce, potem w Excelu.

Wariancja i odchylenie standardowe w pracy magisterskiej

Zacznijmy od obrazu: masz średnią, wokół niej krążą Twoje wyniki. Chcesz wiedzieć, jak bardzo się rozbiegają. Najpierw liczysz „rozbieg” w kwadracie (to będzie wariancja), a potem robisz z tego pierwiastek i wracasz do normalnych jednostek (to będzie odchylenie standardowe). Koniec filozofii. Teraz wersja „na spokojnie”.

Dlaczego najpierw kwadraty, a potem pierwiastek?

1. Różnice względem średniej mają znaki plus/minus i wzajemnie się znoszą. Po podniesieniu do kwadratu wszystkie są dodatnie.
2. Kwadrat mocniej „kara” duże odchylenia (outliery), więc wariancja „widzi” rozstrzelone dane.
3. Problem: wariancja ma kwadratowe jednostki (zł², min², pkt²). Dlatego bierzemy pierwiastek → dostajemy odchylenie standardowe (SD) w tych samych jednostkach, co dane. I to jest miara, którą da się intuicyjnie przeczytać: „SD = 6 minut”.

Wzory (to naprawdę wszystko)

• Populacja (gdy masz wszystkie elementy, rzadko w pracach):

Wariancja

Odchylenie standardowe

• Próba (gdy masz fragment populacji – czyli typowa praca dyplomowa):

Wariancja

Odchylenie standardowe

„Kwadrat odchylenia standardowego” = wariancja. Zawsze.

Ale czemu w próbie dzielimy przez n−1, a nie przez n?

To słynna poprawka Bessela. Intuicja: średnią x szacujesz z tych samych danych, więc „przylega” do nich zbyt mocno i naturalnie zaniża rozproszenie. Dzieląc przez n−1, korygujesz stronniczość i dostajesz lepszy (bezstronny) estymator wariancji populacji.

Wersja na chłopski rozum: gdy znasz n−1n odchyleń, ostatnie jest wymuszone (musi „zamknąć” sumę odchyleń do zera), więc faktycznie masz tylko n−1 „stopni swobody”.

Mini-przykład (z kalkulatorem w głowie)

Weź dane: 2, 4, 4, 4, 5, 5, 7, 9

• Średnia xˉ=5
• Odchylenia od średniej: −3,−1,−1,−1,0,0,2,4
• Kwadraty: 9,1,1,1,0,0,4,16 Suma = 32.

Gdyby to była populacja (σ):

A dla próby (s) – realny scenariusz w pracy:

Wniosek: s jest zwykle trochę większe od σ, bo próba „niedoszacowuje” zmienności i trzeba ją lekko „podbić” przez n−1.

Odchylenie standardowe a wariancja – kiedy którą miarę cytować?

• Wariancja jest wygodna w matematyce, modelach i ANOVA (bo „sumuje się” ładniej).
• SD jest wygodne w czytaniu: ta sama jednostka co dane, łatwa interpretacja w raporcie („M = 72 pkt, SD = 6,3 pkt”).
• W praktyce: w wynikach najczęściej raportujesz średnią ± SD; w metodach/analizie możesz mówić o wariancji, bo to z niej bierze się SD.

Jak obliczyć odchylenie standardowe w pracy magisterskiej. Krok po kroku (ręcznie)

Zasada ogólna (plan działania)

Dane → średnia → odchylenia od średniej → kwadraty → suma → / (N lub n−1) → pierwiastek.

• Gdy traktujesz dane jak populację (rzadko w pracach) → dzielisz przez N.
• Gdy traktujesz jak próbę (typowo w pracy) → dzielisz przez n−1 (poprawka Bessela).

Przykład A: małe SD (bez outlierów)

Dane: 12, 13, 11, 12, 12, 13, 11, 12 (n = 8)

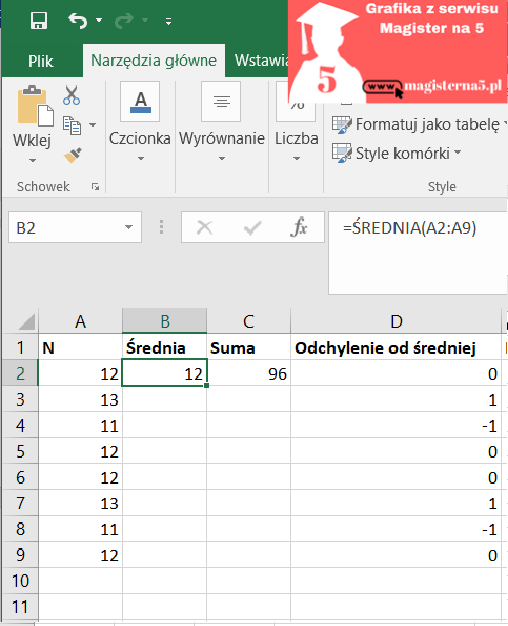
1. Średnia (x̄):
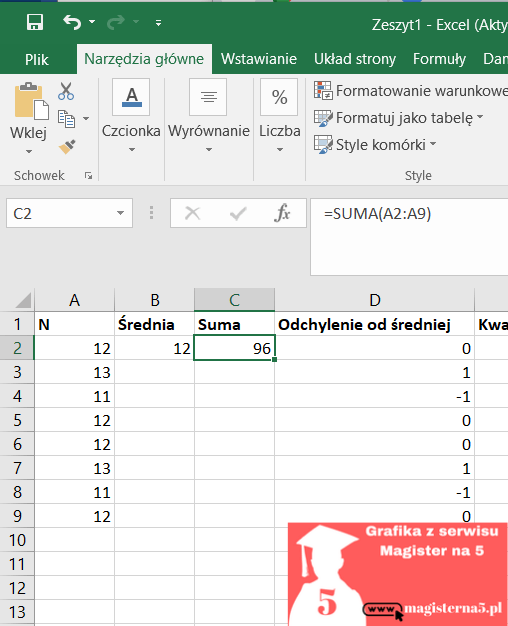
   Suma = 12+13+11+12+12+13+11+12 = 96

x̄ = 96 / 8 = 12,000

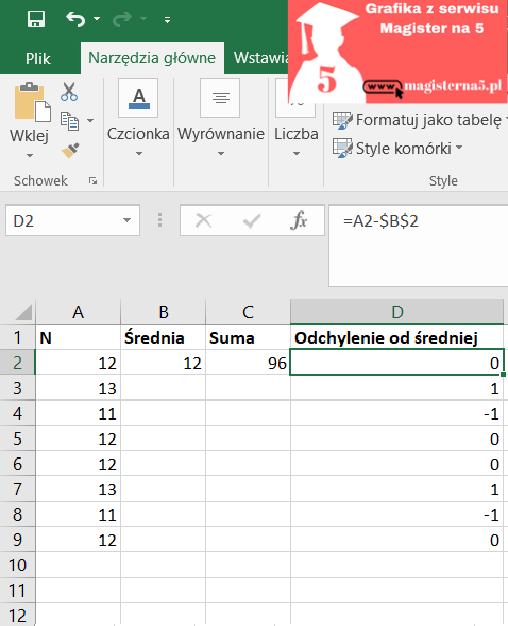
1. Odchylenia od średniej (xi − x̄):

• 12 − 12 = 0,000
• 13 − 12 = 1,000
• 11 − 12 = −1,000
• 12 − 12 = 0,000
• 12 − 12 = 0,000
• 13 − 12 = 1,000
• 11 − 12 = −1,000
• 12 − 12 = 0,000

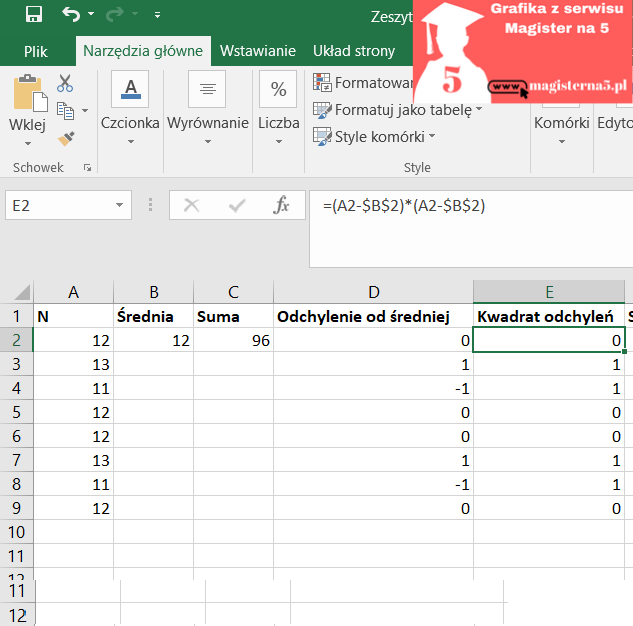
1. Kwadraty odchyleń ( (xi − x̄)² ):
   0,000; 1,000; 1,000; 0,000; 0,000; 1,000; 1,000; 0,000

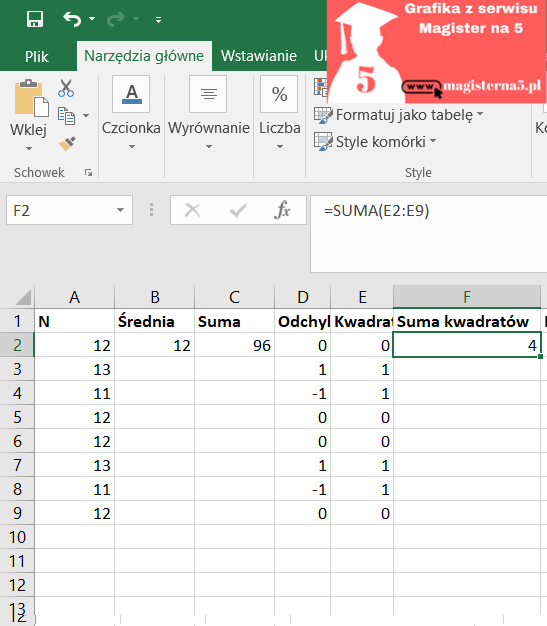
Suma kwadratów = 4,000

1. Wariancja i SD:

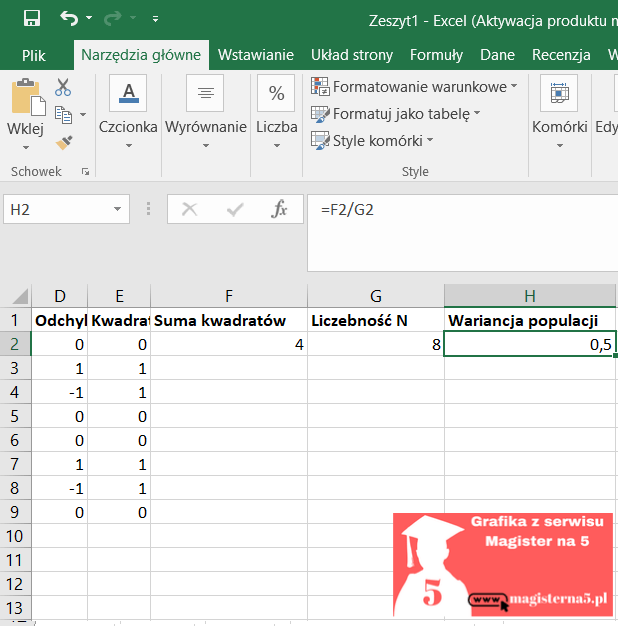
• Populacja: σ² = 4,000 / 8 = 0,500

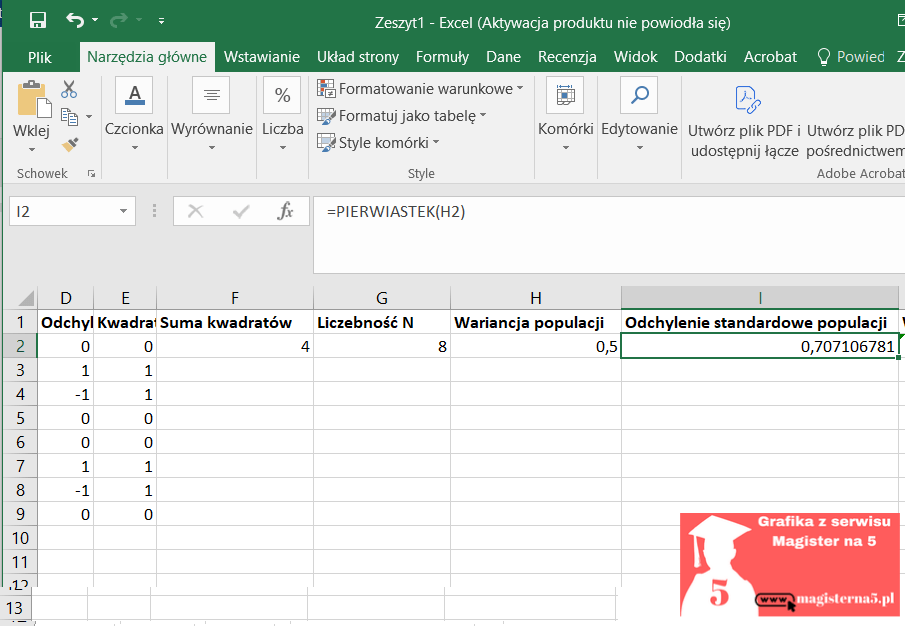
•  0,500→ σ = √0,500 = 0,707106…

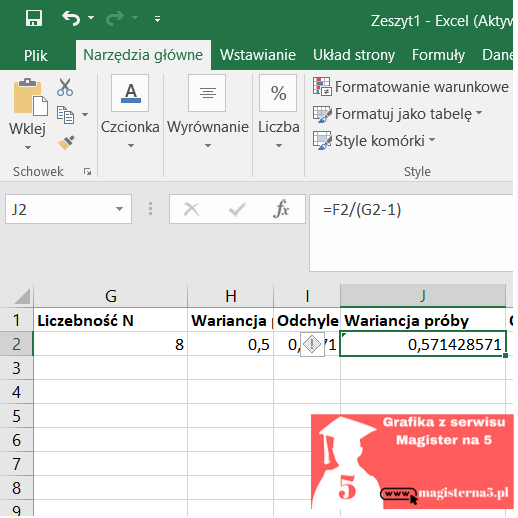
• Próba: s² = 4,000 / 7 = 0,571428…

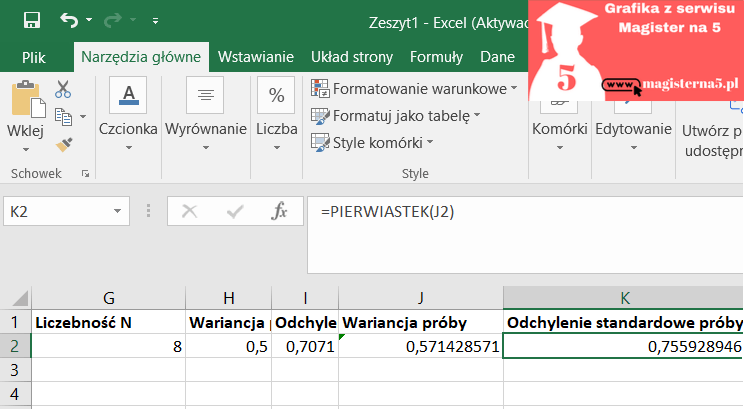
• 0,571428… → s = √0,571428… = 0,755929…

Wniosek: dane są „zbite” wokół średniej — SD jest małe (ok. 0,71 populacyjnie i 0,76 dla próby).

Plik do liczenia odchylenia standardowego w Excelu

Chcesz się sprawdzić w Excelu?

Przygotowaliśmy plik z arkuszem, gdzie masz wszystkie powyższe dane i wzory. Możesz podmienić dane i zobaczyć, jak zmienia się SD.

Pobierz:Plik excel odchylenie standardowe

Przykład B: duże SD (z jednym outlierem)

Dane: 12, 13, 11, 12, 12, 13, 11, 12, 35 (n = 9)

1. Średnia (x̄):
   Suma = 12+13+11+12+12+13+11+12+35 = 131
   x̄ = 131 / 9 = 14,555556
2. Odchylenia (xi − x̄) — zaokrąglone do 3 miejsc:

• 12 − 14,555556 = −2,556
• 13 − 14,555556 = −1,556
• 11 − 14,555556 = −3,556
• 12 − 14,555556 = −2,556
• 12 − 14,555556 = −2,556
• 13 − 14,555556 = −1,556
• 11 − 14,555556 = −3,556
• 12 − 14,555556 = −2,556
• 35 − 14,555556 = 20,444

1. Kwadraty ( (xi − x̄)² ) — do 3 miejsc:
   6,531; 2,420; 12,642; 6,531; 6,531; 2,420; 12,642; 6,531; 417,975
   Suma kwadratów = 474,222222
2. Wariancja i SD:

• Populacja: σ² = 474,222222 / 9 = 52,691358 → σ = √52,691358 = 7,258881…
• Próba: s² = 474,222222 / 8 = 59,277778 → s = √59,277778 = 7,699206…

Odchylenie standardowe w Excelu – praktyczny poradnik

W Excelu oprócz ręcznego liczenia możesz do obliczyć odchylenie standardowe za pomocą funkcji.

Funkcje z Excela, które potrzebujesz do liczenia odchylenia standardowego

Poniższe wzory możesz skopiować do swojego pliku w Excelu i wykorzystać:

• SD z próby: =ODCH.STANDARD.PRÓBKI(A2:A9)
• SD populacji: =ODCH.STANDARD.POPUL(A2:A9)
• SE: =ODCH.STANDARD.PRÓBKI(A2:A9)/PIERWIASTEK(ILE.LICZB(A2:A9))
• %RSD: =ODCH.STANDARD.PRÓBKI(A2:A9)/ŚREDNIA(A2:A9)
• Suma kwadratów odchyleń: =ODCH.KWADRATOWE(A2:A9)

Pobierz :

Plik excel odchylenie standardowe gotowiec

W tym pliku masz gotowe wszystkie niezbędne funkcje, wystarczy ze wstawisz swoje dane w kolumnę N, (ewentualnie zwiększysz zakres z A9 do innej potrzebnej wartości np. A50, A100 itp. -Zależy, ile masz danych i gotowe.

Okej, ale co oznaczają te formuły i jak ich używać?

1) =ODCH.STANDARD.PRÓBKI(A2:A9) — odchylenie standardowe z próby (SD, „s”)

Co to jest?

Miara rozrzutu danych wokół średniej w próbie (fragment populacji). Liczone ze „stopniami swobody” → w mianowniku jest (n−1) (tzw. poprawka Bessela).

Kiedy używać?

W praktycznie każdej pracy studenckiej, gdy masz zebrane dane od pewnej grupy (a nie od całej populacji).

Interpretacja:

• Małe SD → wartości są blisko średniej (stabilność).
• Duże SD → wartości mocno się różnią (zmienność/ryzyko).
• Jednostki: takie jak dane (minuty, zł, punkty), więc łatwo „czuć skalę”.

Jak opisać w pracy (wyniki):

„Średnia (M) liczba punktów wyniosła 72, SD = 6,3 (n = 58).”
„Zmienność wyników była umiarkowana; wartości skupiały się w okolicach średniej.”

2) =ODCH.STANDARD.POPUL(A2:A9) — odchylenie standardowe populacji (SD, „σ”)

Co to jest?

SD liczone tak, jakby dane obejmowały całą populację (w mianowniku N).

Kiedy używać?

Rzadko w pracach, tylko jeśli naprawdę mierzysz całość (np. wszyscy studenci jednego, małego roku).

Interpretacja: Analogiczna do PRÓBKI, ale otrzymasz zwykle trochę mniejszą wartość (bo dzielisz przez N, a nie n−1).

Jak opisać (metody):

„Dla opisu rozrzutu w populacji obliczono odchylenie standardowe populacyjne (ODCH.STANDARD.POPUL).”

3) =ODCH.STANDARD.PRÓBKI(A2:A9)/PIERWIASTEK(ILE.LICZB(A2:A9)) — SE (błąd standardowy średniej)

Co to jest?

Szacuje, jak bardzo średnia z próby (M) może się wahać przy losowaniu kolejnych prób tej samej wielkości.

Kiedy używać?

Gdy pokazujesz precyzję średniej, budujesz przedziały ufności dla średniej albo tworzysz wykresy średnia ± SE.

Interpretacja: Mniejsze SE = średnia oszacowana dokładniej (zwykle większa próba → mniejsze SE).

Związek: SE = SD / √n.

Jak opisać (wyniki):

„Średnia (M) = 72 ± 1,1 SE (n = 58).”
„Precyzję oszacowania średniej oceniono za pomocą błędu standardowego.”

4) =ODCH.STANDARD.PRÓBKI(A2:A9)/ŚREDNIA(A2:A9) → %RSD (względne SD)

Co to jest?

SD wyrażone względem średniej (często w %).

Kiedy używać?

Gdy porównujesz zmienność między różnymi skalami (np. zł vs. min) albo gdy ważna jest precyzja pomiaru (chemia/analityka).

Interpretacja: Np. %RSD = 4,5% → „SD stanowi 4,5% średniej” (relatywnie niski rozrzut).

Jak opisać (wyniki):

„Względna zmienność wyniosła %RSD = 4,5%, co wskazuje na dobrą powtarzalność pomiarów.”

5) =ODCH.KWADRATOWE(A2:A9) — suma kwadratów odchyleń (DEVSQ)

Co to jest?

∑(xi−xˉ)2\sum (x_i – \bar{x})^2∑(xi​−xˉ)2. Surowy „wkład” do wariancji/SD przed podzieleniem przez N lub (n−1).

Kiedy używać?

• Gdy chcesz ręcznie policzyć wariancję/SD:
  • wariancja populacyjna: =ODCH.KWADRATOWE(zakres)/N
  • wariancja próby: =ODCH.KWADRATOWE(zakres)/(N-1) → potem pierwiastek.
• W bardziej zaawansowanych analizach (ANOVA, regresja) jako element obliczeń.

Jak opisać (metody):

„Dla przejrzystości obliczeń pokazano również sumę kwadratów odchyleń (DEVSQ), z której wyprowadzono wariancję i odchylenie standardowe.”

Kiedy której miary używać (błyskawiczna ściąga)

Interpretacja i przykłady z życia odchylenia standardowego

Odchylenie standardowe (SD) mówi, jak bardzo Twoje liczby rozchodzą się wokół średniej.
Małe SD = wszystko podobne. Duże SD = każdy „leci” w swoją stronę.
I tyle. Serio.

Zasada 68–95–99,7% (gdy dane są „w miarę normalne”)

Wyobraź sobie dzwonowaty wykres. W takim układzie:

• ok. 68% wyników wpada w średnia ± 1×SD,
• ok. 95% w średnia ± 2×SD,
• ok. 99,7% w średnia ± 3×SD.
  Czyli znając średnią i SD, wiesz, gdzie leży większość danych.
  Uwaga: jeśli masz mocno skośne dane albo odlotowe wartości, ta reguła działa słabiej. Wtedy patrz też na medianę + IQR.

Jak to napisać w pracy  dyplomowej?

• Opis miary:
  „Zmienność opisano odchyleniem standardowym (SD); interpretację oparto na regule 68–95–99,7% dla danych zbliżonych do normalnych.”
• Przykład – dojazdy:
  „M = 24 min, SD = 6 min. Około 68% studentów dojeżdża 18–30 min.”
• Przykład – test:
  „M = 50 pkt, SD = 5 pkt. Wyniki ≥ 60 pkt są ok. 2×SD powyżej średniej.”
• Przykład – inwestycje:
  „Obie strategie miały M = 1%/mies., lecz strategia B miała większą zmienność (SD = 6% vs 2%), co oznacza wyższe ryzyko.”
• Zastrzeżenie przy skośności:
  „Przy danych skośnych lub z outlierami raportowano też medianę i IQR.”

I tyle. Teraz patrzysz na M i SD i w 3 sekundy wiesz, czy dane są „spokojne”, czy „dzikie”.

Jak wykorzystać odchylenie standardowe (SD) w pracy dyplomowej? Kiedy tak, kiedy nie

Pomyśl o SD jak o linijce do mierzenia „rozjechania” wyników wokół średniej. Jeśli Twoje dane są w miarę gładkie (bez wielkich odchyleń i bez mocnej skośności), SD działa świetnie. Wtedy najczytelniejszy zapis w pracy to po prostu „M ± SD”. Np.: „Czas reakcji wyniósł 320 ms ± 18 ms (SD).” Czytelnik od razu widzi i poziom, i rozrzut – w tych samych jednostkach.

Kiedy to ma sens? Gdy porównujesz średnie między grupami i spełniasz podstawowe założenia statystyki klasycznej (w skrócie: dane są „w miarę normalne”). Przykład: dwa roczniki, ta sama skala punktów, podobna liczebność. Wtedy SD opowiada wiarygodną historię o zmienności. Jeśli chcesz pokazać, jak dokładnie oszacowałeś średnią, dołóż błąd standardowy średniej (SE). To prosta relacja: SE = SD / √n. SE nie opisuje rozrzutu pojedynczych wyników, tylko niepewność średniej. Do wniosków typu „czy grupy różnią się istotnie” wykorzystujesz zwykle test t (o ile założenia są OK).

Kiedy nie iść w SD? Kiedy rozkład jest skośny albo masz odstające rekordy (np. jedna osoba z kosmicznym czasem dojazdu lub bardzo wysoką pensją). Wtedy SD rośnie, ale nie mówi prawdy o „typowym” przypadku. Tu lepszy jest duet mediana + IQR (rozstęp międzykwartylowy). W pracy napiszesz wtedy np.: „Ze względu na skośność rozkładu raportowano medianę (Me) i IQR; różnice oceniano testem Manna–Whitneya.” Proste i uczciwe.

Jak to ogarnąć technicznie, bez wchodzenia w teorię? Rzuć okiem na histogram albo boxplot. Jeśli widzisz ładny „dzwon” i brak długich ogonów – M ± SD będzie OK. Jeśli widzisz ogon lub pojedyncze „gwiazdy” daleko od reszty – przełącz się na Me + IQR. W dwóch zdaniach w „Metodach” napisz, dlaczego wybrałeś tę, a nie inną miarę. Promotor to doceni.

Jak to ładnie opisać w „Wynikach”? Oto dwa wzory zdań, które możesz podstawić pod swoje liczby:

Do wykresów wybierz to, co pasuje do miary. Dla M ± SD sprawdzą się słupki z błędami (±SD). Dla Me + IQR – boxplot. Nie mieszaj ich na jednym rysunku, bo to męczy oko i myli czytelnika.

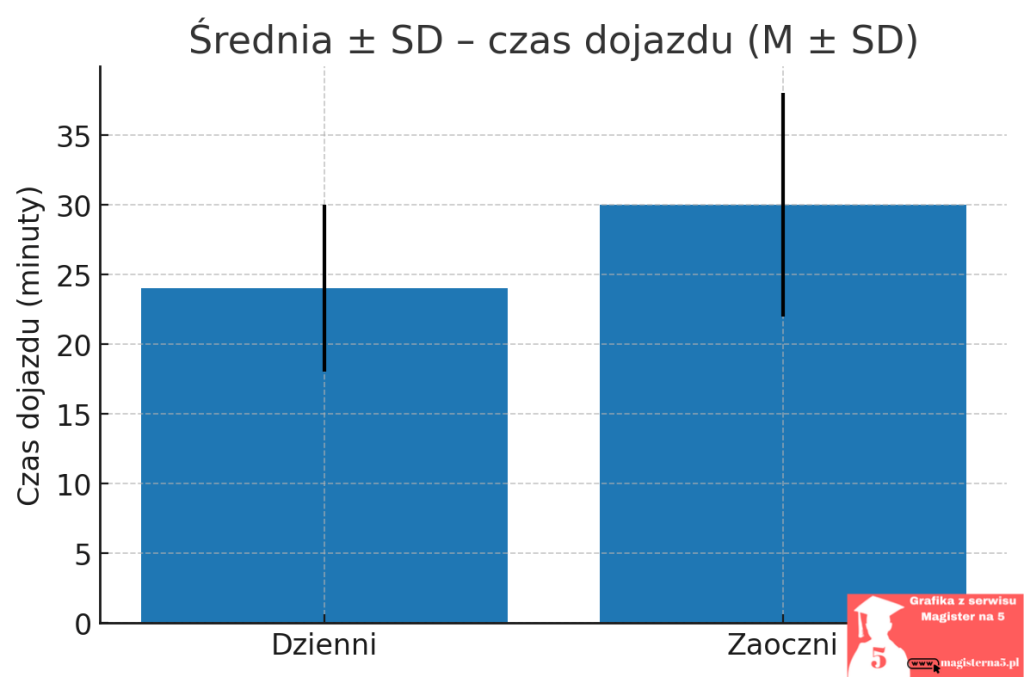
Poniżej znajdują się dwa przykładowe wykresy: słupki z błędami i boxplot.

Na pierwszym rysunku zrobiliśmy wykres M ± SD. Każdy słupek pokazuje średni czas dojazdu w grupie, a cienkie „wąsy” nad słupkiem to odchylenie standardowe. Widać, że studenci dzienni mają średnio krótszy dojazd (około 24 min), a zaoczni dłuższy (około 30 min). Wąsy są też wyraźnie dłuższe u zaocznych, co znaczy, że ich czasy bardziej się rozjeżdżają – jedni jadą szybko, inni bardzo długo. Ten wykres odpowiada na pytanie „jaki jest poziom w grupie i jak bardzo wyniki wahają się wokół średniej”. Dobrze sprawdza się, gdy rozkład jest w miarę „normalny”.

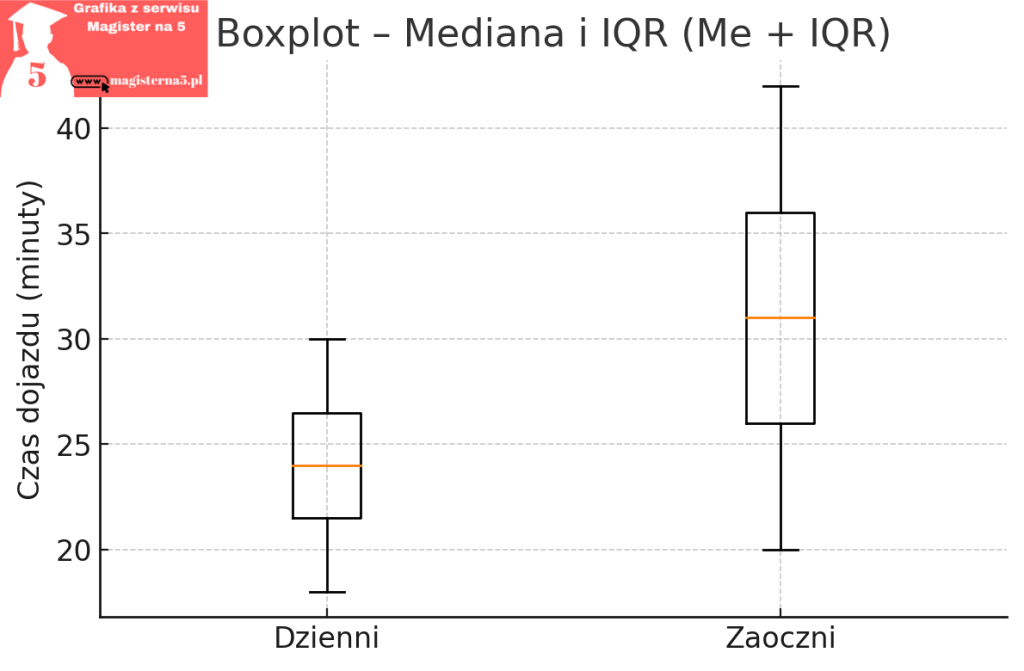
Na drugim rysunku mamy boxplot, czyli obraz mediany i IQR. Pozioma linia w pudełku to mediana – w praktyce „typowy” wynik. U dziennych mediana to około 24 min, u zaocznych około 31 min, więc typowy zaoczny dojeżdża dłużej. Szerokość pudełka to IQR (od Q1 do Q3), czyli „gruby środek” danych. Pudełko u zaocznych jest szersze, co od razu mówi, że w tej grupie jest większe zróżnicowanie w środku rozkładu. Wąsy sięgają poza pudełko i pokazują typowy zasięg poza IQR; jeśli pojawiłyby się pojedyncze kropki daleko od wykresu, byłyby to obserwacje odstające. Ten wykres jest najlepszy, gdy dane są skośne albo masz podejrzenie, że są „dziwne” rekordy – skupia się na środku i nie daje się łatwo oszukać skrajnościami.

Oba rysunki opowiadają tę samą historię z dwóch perspektyw. M ± SD mówi: „średnio tyle i tak bardzo się waha”. Boxplot mówi: „typowo tyle, a środek danych ma taką szerokość”. W naszych przykładach wniosek jest prosty: zaoczni jeżdżą dłużej i mniej równo niż dzienni.

I na koniec dwie ważne przestrogi w jednym zdaniu: Nie myl SD (odchylenie standardowe, ang. standard deviation) z SE (błąd standardowy średniej, ang. standard error) i pamiętaj, że w pracy najczęściej raportujesz SD z próby, a nie populacyjne.

Dla pełnej jasności: SD opisuje rozrzut pojedynczych wyników wokół średniej (ta sama jednostka co dane), a SE opisuje niepewność oszacowania średniej i zwykle liczymy je jako SE = SD/√n (maleje, gdy rośnie liczebność próby).

Najczęstsze błędy związane z odchyleniem standardowym w pracy magisterskiej

• Mylenie SD z SE. SD (odchylenie standardowe) opisuje rozrzut pojedynczych wyników wokół średniej, a SE (błąd standardowy średniej) mówi, jak dokładnie oszacowana jest sama średnia; raportuj M ± SD, gdy pokazujesz zmienność danych, a SE = SD/√n używaj do precyzji średniej lub przedziałów ufności.
• Zły wariant funkcji: populacja vs próba. W pracach niemal zawsze masz próbę, więc licz i podawaj SD z próby (np. ODCH.STANDARD.PRÓBKI / STDEV.S), a wersji populacyjnej (ODCH.STANDARD.POPUL / STDEV.P) używaj tylko wtedy, gdy naprawdę masz całą populację.
• SD na skali Likerta (1–5). To skala porządkowa, więc średnia i SD potrafią wprowadzić w błąd; lepiej pokaż medianę (Me) i IQR albo odsetki odpowiedzi, a SD stosuj dopiero przy wiarygodnej skali sumarycznej zachowującej się jak liczba.
• Brak jednostek. SD ma te same jednostki co dane, więc pisz „SD = 6 min” zamiast „SD = 6”; czytelnik od razu rozumie skalę.
• Mieszanie miar na jednym wykresie. Nie łącz na jednym rysunku M ± SD z Me + IQR — zrób dwa osobne wykresy: słupki z błędami dla średniej oraz boxplot dla mediany i IQR.
• Ignorowanie skośności i outlierów. Przy wyraźnie skośnych danych lub pojedynczych rekordach „odjechanych” w bok samo SD puchnie i gubi sens typowości; wtedy raportuj równolegle Me + IQR i pokaż boxplot.
• Za mała próba. Przy bardzo małym n (np. 5–10) SD bywa niestabilne; pokaż też pojedyncze obserwacje, podaj Me + IQR i zachowaj ostrożność w wnioskach.
• Testy bez sprawdzenia założeń. Jeśli raportujesz M ± SD i różnice testem t/ANOVA, rzuć okiem na histogram/QQ-plot i jednorodność wariancji; gdy założenia nie trzymają, przejdź na testy nieparametryczne.
• Niejasny wybór miary. Zawsze jednym zdaniem wyjaśnij, dlaczego używasz SD (dane ~normalne, interesuje Cię średnia) albo Me + IQR (skośność/outliery); promotor i recenzent to docenią.

Pamiętaj, że SD ≠ SE, w pracy najczęściej raportujesz SD z próby, podawaj jednostki, dobieraj wykres do miary i krótko uzasadnij wybór. Dzięki temu Twoje wyniki będą jasne, spójne i „do obrony”.

Odchylenie standardowe w pracy magisterskiej podsumowanie

Odchylenie standardowe to po prostu miarka, która mówi, czy Twoje wyniki są raczej zebrane w kupie, czy rozbiegają się na wszystkie strony.

Gdy jest małe — masz spokój i przewidywalność; gdy duże — szykuj się na niespodzianki. Weź swoje prawdziwe dane: dojazdy, oceny, wydatki na kawę i zobacz, jak bardzo skaczą — od razu poczujesz, czy bliżej Ci do zen, czy do rollercoastera. A jeśli coś nie gra albo chcesz to ładnie wstawić do pracy, odezwij się — Magister na 5 pomoże ogarnąć liczby, dopracować wykresy i dociągnąć całość na piątkę.

Trochę już wiem o odchyleniu standardowych w pracy magisterskiej. Teraz chcę poznać proces pisania

Naucz się pisać pracę w godzinę. Sprawdź e-book.

Zobacz, jakie materiały mogę Ci jeszcze zaproponować.
–>Sklep Magistra na 5

Jeżeli potrzebujesz pomocy, po prostu napisz.
–> Wyślij pytanie

Nie zapomnij o prezencie!