Siła efektu w statystyce (effect size). Szybki poradnik

Ostatnia aktualizacja 8 października 2025

Masz „p < 0,05” i… co dalej? Czy to wielki przełom, czy tylko mikroskopijna różnica, której nikt nie zauważy w realu? Tu wchodzi siła efektu — liczba, która nie pyta „czy coś jest”, tylko „jak bardzo”. Dzięki niej odróżnisz wynik „statystycznie istotny” od istotnego w praktyce.

W tym krótkim poradniku w 5 minut ogarniesz, co to jest siła efektu, po co ją podawać w pracy dyplomowej, jak policzyć ją w jamovi na dwa kliknięcia i jakie progi warto mieć na ściągawce. Zero żargonu, same konkrety — żebyś mógł/mogła napisać „Wyniki”, które naprawdę robią wrażenie na promotorze.

Potrzebujesz szybkiej pomocy z obliczeniami statystycznymi w swojej pracy dyplomowej? Kliknij poniżej
–> Statystyka do pracy magisterskiej. Błyskawiczna pomoc
–> Wzory rozdziałów badawczych ze statystyką

Nie wiem, jak zacząć. Masz coś dla mnie?
–> E-book- Jak Napisać Pracę Dyplomową W Tydzień
–> Pobierz przykładową pracę licencjacką

Definicja siły efektu statystycznego

Siła efektu to liczba, która mówi nie „czy coś jest”, tylko jak bardzo. Innymi słowy: czy różnica/związek to słoń, kot, czy raczej mysz. Dzięki niej wiesz, czy wynik ma sens w praktyce, a nie tylko „wyszedł p<0,05”.

Najczęstsze miary — w wersji „do przeżycia”:

d Cohena (różnice średnich, testy t)
Myśl: o ile „standardowych odchyleń” różnią się grupy.

r / R² (korelacje, regresje)
r mówi, jak silny i w jakim kierunku jest związek (−1 do 1). R² mówi, ile procent zmienności wyjaśnia model.

η² częściowe (ηp²) (ANOVA)
Jaki procent różnic w wynikach „idzie na konto” badanego czynnika.

OR / RR (iloraz szans / ryzyko — medycyna)
„Ile razy większe/mniejsze” są szanse lub ryzyko w jednej grupie względem drugiej.

Po co siła efektu statystycznego w pracy dyplomowej?

Bo p mówi tylko „czy coś widać”, a siła efektu dopowiada „jak bardzo to widać”. Dzięki temu nie kończysz na suchym „wyszło/nie wyszło”, tylko pokazujesz, czy różnica ma sens w realu (duża, średnia, czy malutka). To od razu ułatwia wnioski praktyczne i rozmowę z promotorem: można sensownie powiedzieć, co oznacza wynik poza tabelką.

Siła efektu przydaje się też przed zebraniem danych — jest potrzebna do planowania mocy testu i liczebności próby (ile osób musisz przebadać, żeby w ogóle mieć szansę zobaczyć to, czego szukasz).

Jak obliczyć siłę efektu statystycznego w Jamovi 

1) d Cohena (test t dla dwóch grup) — stres ~ tryb

Kroki:

• Analizy → Testy t → Niezależne próbki t.
• Przenieś stres do pola Zmienne zależne (już masz).
• Przenieś tryb (Dzienni/Zaoczni) do Zmienna grupująca (już masz).
• W panelu po lewej znajdź sekcję Dodatkowe statystyki i kliknij w kwadracik „Wielkość efektu”.
• Po zaznaczeniu możesz też kliknąć obok „Przedział ufności 95%” (stanie się aktywny).
• Warto włączyć „Statystyki opisowe” i „Test homogeniczności (Levene’a)” niżej – ułatwia to opis.
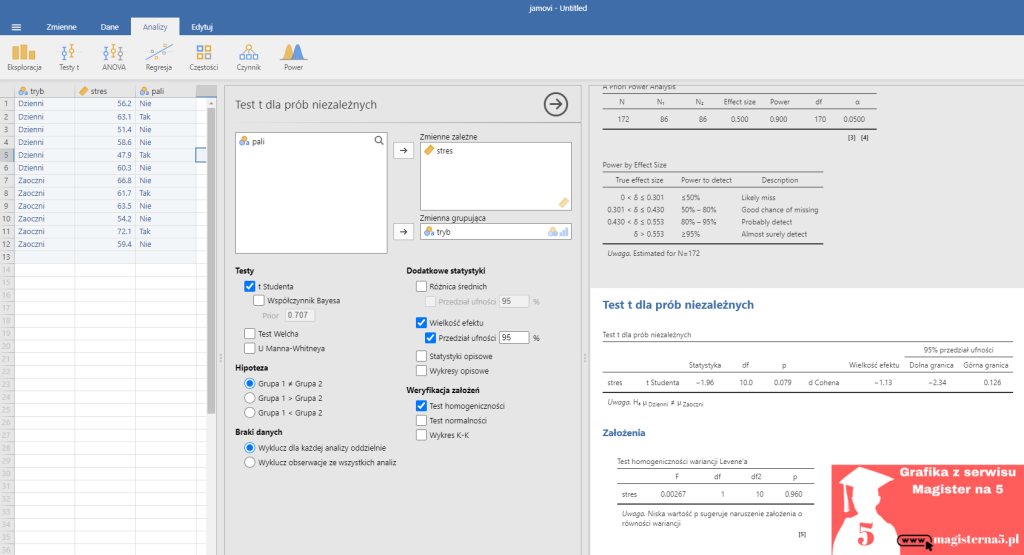
• Po prawej, pod tabelą „Test t dla prób niezależnych”, pojawi się osobna tabela „Wielkość efektu” z d Cohena i (jeśli włączyłaś/eś) 95% przedziałem ufności.

Jak czytać siłę efektu statystycznego w wynikach Twoich badań?

Test t dla prób niezależnych (stres ~ tryb):

• t = −1,96, df = 10, p = 0,079 → przy α = 0,05 brak wystarczających dowodów na różnicę średnich.
• d Cohena = −1,13, 95% PU: −2,34 do 0,126 → oszacowanie sugeruje duży efekt, ale przedział obejmuje 0, więc wynik jest niepewny (mała próba).
• Test Levene’a: p = 0,960 → założenie równości wariancji spełnione.

Znak minus przy t i d oznacza, że średnia Grupy 1 (u Ciebie prawdopodobnie „Dzienni”) jest niższa niż Grupy 2 („Zaoczni”). Czyli trend: zaoczni mają wyższy stres – ale przy tym N dowody są za słabe (p=0,079).

Jak siłę efektu statystycznego wpisać w pracy dyplomowej (gotowiec – podmień tylko etykiety grup, jeśli trzeba)

Wynik + siła efektu:
„Poziom stresu nie różnił się istotnie między studentami zaocznymi i dziennymi, t(10) = −1,96, p = 0,079. Oszacowana siła efektu była duża, d Cohena = −1,13 (95% PU: −2,34 do 0,13), jednak szeroki przedział ufności obejmuje 0, co wskazuje na niepewność wyniku.”

Założenia:
„Założenie równości wariancji było spełnione (test Levene’a: p = 0,960).”

Krótki komentarz (opcjonalnie):
„Mała liczebność (ok. 6 osób na grupę) oznacza niską moc testu, więc wynik nieistotny należy interpretować ostrożnie; w kolejnych badaniach warto zwiększyć N.”

Mini-ściąga interpretacyjna (do marginesu)

Progi „siły efektu”

• d Cohena (różnice średnich): 0,20 mały | 0,50 średni | 0,80 duży
  (znak „−” = Grupa 1 ma niżej niż Grupa 2)
• r (korelacja): 0,10 mała | 0,30 średnia | 0,50 duża
  R² = % wyjaśnionej zmienności (np. R²=0,25 → 25%).
• ηp² (ANOVA): 0,01 mały | 0,06 średni | 0,14 duży
• Cramér’s V (kategoria×kategoria): 0,10 mały | 0,30 średni | 0,50 duży
• OR/RR (medycyna): =1 brak efektu; >1 większe ryzyko/szanse, <1 mniejsze
  (np. OR≈1,5 – umiarkowanie; OR≥2 – duży, ale kontekst ma znaczenie).

Przedziały ufności (95%)

• Różnice/korelacje: jeśli obejmuje 0 → dowody słabe; im węższy, tym pewniej.
• OR/RR: jeśli obejmuje 1 → dowody słabe.

p-value i moc (w pigułce)

• p < 0,05 → są dowody na efekt; p ≥ 0,05 → brak mocnych dowodów (to nie „dowód, że efektu nie ma”).
• Moc: celuj w 0,80; niska moc = ryzyko przegapienia efektu.

Gotowe. Teraz odpal jamovi, zaznacz siłę efektu + 95% PU i wstaw jedno z powyższych zdań do „Wyników”.

Siła efektu statystycznego zakończenie

Siła efektu to Twoje „ile tego jest” — bez niej wyniki brzmią jak plotka, z nią jak solidny raport. Dzięki jednej liczbie (plus 95% przedział ufności) wiesz, czy różnica jest mikra, średnia czy konkretna, a promotor widzi, że nie tylko „wyszło p<0,05”, ale też ma to sens w praktyce.

Na koniec prosta recepta: w Jamovi kliknij test → zaznacz siłę efektu + 95% PU → w „Wynikach” wpisz statystykę + p + efekt + PU i dodaj jedno zdanie, co to znaczy „po ludzku”. Koniec magii. Twoja praca staje się czytelna, rzetelna i — co najważniejsze — obroni się nie tylko na komisji, ale i w realnym świecie.

Trochę już wiem o sile efektu statystycznego w  pracy magisterskiej. Teraz chcę poznać proces pisania

Naucz się pisać pracę w godzinę. Sprawdź e-book.

Zobacz, jakie materiały mogę Ci jeszcze zaproponować.
–>Sklep Magistra na 5

Jeżeli potrzebujesz pomocy, po prostu napisz.
–> Wyślij pytanie

Nie zapomnij o prezencie!