Ostatnia aktualizacja 12 sierpnia 2025
Wyobraź sobie, że robisz wykres punktowy, na którym pokazujesz, ile godzin ktoś śpi i jaki ma poziom stresu. Punkty są rozrzucone, ale… da się przez nie poprowadzić prostą linię, która mniej więcej pokazuje ogólną tendencję: im więcej snu, tym mniej stresu. I właśnie ta linia to w dużym skrócie regresja liniowa – taki „matematyczny detektyw”, który szuka prostego wzoru na zależność między dwiema rzeczami.
Możesz o niej myśleć, jak o „linii trendu” w Excelu, tylko w wersji na poważnie – z liczbami, które pozwalają przewidzieć, co może się wydarzyć.
W pracy dyplomowej regresja liniowa pomoże Ci odpowiedzieć na pytania typu: „Czy X wpływa na Y?” albo „O ile zmieni się Y, jeśli X wzrośnie o 1?”. To narzędzie jest proste, ale potrafi powiedzieć naprawdę sporo – pod warunkiem że użyjesz go we właściwym momencie.
Potrzebujesz szybkiej pomocy z policzeniem regresji liniowej do swojej pracy dyplomowej? Kliknij poniżej
–> Regresja liniowa do pracy magisterskiej. Błyskawiczna pomoc
–> Wzory rozdziałów badawczych ze statystyką
Nie wiem, jak zacząć. Masz coś dla mnie?
–> E-book- Jak Napisać Pracę Dyplomową W Tydzień
–> Pobierz przykładową pracę licencjacką

Regresja liniowa w pracy magisterskiej- kiedy się przydaje?
Wyobraź sobie, że regresja liniowa to taki akademicki GPS – jeśli dasz mu dobrą mapę (czytaj: dane), to pokaże Ci, w którą stronę zmierza Twoja zależność. Ale jeśli wrzucisz mu chaos, dziury w drodze i kilka skrzyżowań bez znaków, to… skończysz w polu.
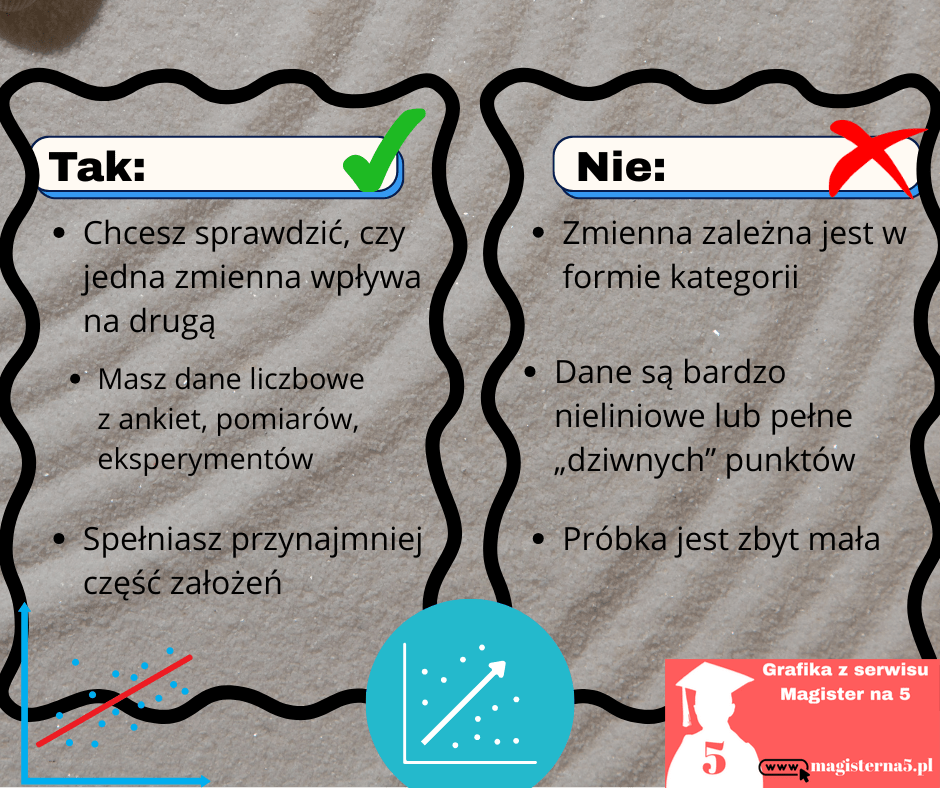
✅ Tak, gdy:
- Chcesz sprawdzić, czy jedna zmienna wpływa na drugą. Na przykład: „Czy liczba godzin snu zmniejsza poziom stresu?” albo „Czy większa aktywność fizyczna przekłada się na niższe BMI?”. Regresja liniowa odpowiada na takie pytania niemal jak profesor na egzaminie – konkretnie i z liczbami.
- Masz dane liczbowe z ankiet, pomiarów, eksperymentów. Widzisz w tabeli same liczby? To świetny znak – regresja uwielbia cyfry. Im bardziej Twoje dane przypominają uporządkowaną listę wyników, tym lepiej model będzie działał.
- Spełniasz przynajmniej część założeń. Jeśli wykres Twoich danych przypomina w miarę prostą chmurkę punktów z wyraźnym trendem, a nie rysunek wykonany przez przedszkolaka po trzecim kakao – jest szansa, że model zadziała i pokaże sensowną linię.
❌ Nie, gdy:
- Zmienna zależna jest w formie kategorii. Jeśli chcesz przewidywać coś w stylu „tak/nie”, „kobieta/mężczyzna”, „zaliczone/niezaliczone” – regresja liniowa się obrazi. Wtedy trzeba sięgnąć po jej kuzynkę: regresję logistyczną.
- Dane są bardzo nieliniowe lub pełne „dziwnych” punktów. Jeśli Twoje dane idą zygzakiem, w kółko lub przypominają górski szlak – prosta linia nie ma sensu. Model będzie się męczył, a Ty dostaniesz wyniki, które nadają się tylko do kosza.
- Próbka badawcza jest zbyt mała. Jeśli masz pięć obserwacji i chcesz udowodnić wielką teorię – to tak, jakby próbować przewidzieć pogodę na cały rok, patrząc na dwa dni w kalendarzu. Statystyka lubi, kiedy jest z czego liczyć.
 Przykłady tematów prac magisterskich, w których regresja liniowa ma sens
Przykłady tematów prac magisterskich, w których regresja liniowa ma sens
Czasami w pracy dyplomowej potrzebujesz odpowiedzi na pytanie w stylu: „Czy X naprawdę ma wpływ na Y?”. I tu wchodzi regresja liniowa, cała na biało, gotowa pomóc Ci to policzyć. To trochę jak w dobrym kryminale – masz podejrzanego (zmienną niezależną) i chcesz dowiedzieć się, czy faktycznie stoi za wynikiem (zmienną zależną).
Oto kilka przykładów tematów magisterskich, gdzie regresja liniowa sprawdzi sie doskonale?
- Wpływ aktywności fizycznej na BMI – bo może się okazać, że siłownia naprawdę „odejmuje” kilogramy, a nie tylko czas wolny.
- Zależność czasu nauki od wyników egzaminów – im więcej notatek, tym lepsza ocena… a może jednak nie zawsze?
- Powiązanie wieku pracowników z wydajnością pracy – sprawdzenie, czy doświadczenie faktycznie daje przewagę.
- Wpływ liczby godzin spędzonych w mediach społecznościowych na samoocenę – bo Instagram może działać zarówno jak dopalacz, jak i hamulec dla pewności siebie.
- Zależność spożycia kawy od efektywności pracy – ile filiżanek dziennie to magiczna granica produktywności?
- Wpływ wysokości wynagrodzenia na satysfakcję z pracy – czy pieniądze faktycznie kupują szczęście w pracy?
- Związek liczby godzin snu z liczbą popełnianych błędów w pracy – bo może mniej kawy, a więcej spania to lepsza strategia.
- Wpływ ilości reklam w mediach społecznościowych na liczbę kliknięć w ofertę – gratka dla marketingowców.
- Zależność liczby godzin spędzonych na treningu od wyników sportowych – dla studentów AWF-u.
- Powiązanie spożycia fast foodów z wynikami badań krwi – dla dietetyków i osób z zamiłowaniem do statystyki (i burgerów).
Regresja liniowa najlepiej sprawdza się wtedy, gdy masz liczby, trend i chęć odkrycia zależności. Ale pamiętaj – ona pokaże Ci, czy istnieje związek, a nie zawsze udowodni, że to związek przyczynowo-skutkowy. To narzędzie jest jak lupa – powiększa zależność, ale nie mówi, kto ją „spowodował”.
Jak zrobić regresję liniową do pracy magisterskiej w Excelu – krok po kroku
Regresja liniowa w Excelu to trochę jak domowa pizza – prosta do zrobienia, a efekt potrafi zaskoczyć. Wystarczy kilka składników (czytaj: dane), odrobina narzędzi i w kilka minut masz gotowy model, który możesz wkleić do swojej pracy dyplomowej.
Krok 1 – Przygotowanie danych
- W kolumnie A wpisz zmienną niezależną (np. liczba godzin snu).
- W kolumnie B wpisz zmienną zależną (np. poziom stresu).
- Upewnij się, że w wierszu 1 masz nagłówki (Excel je lubi).
- Dane powinny być liczbowe i w miarę kompletne – brakujące wartości mogą zepsuć analizę.
💡 Pro tip: Jeśli Twoje dane pochodzą z ankiety, upewnij się, że odpowiedzi są zakodowane liczbami (np. skala 1–5).
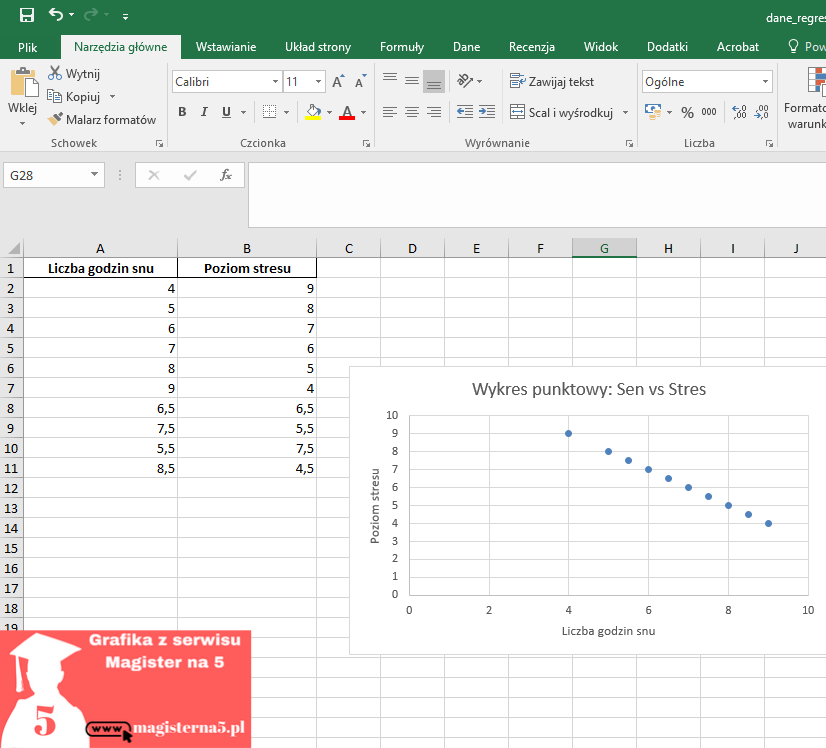
Krok 2 – Wstawienie wykresu punktowego
- Zaznacz obie kolumny danych.
- Wejdź w Wstawianie → Wykres punktowy (XY).
- Wybierz prostą wersję „punkty bez linii” – będzie czytelniej.
💡 Teraz masz wizualizację, która od razu pokaże, czy dane mają w ogóle szansę układać się w linię.
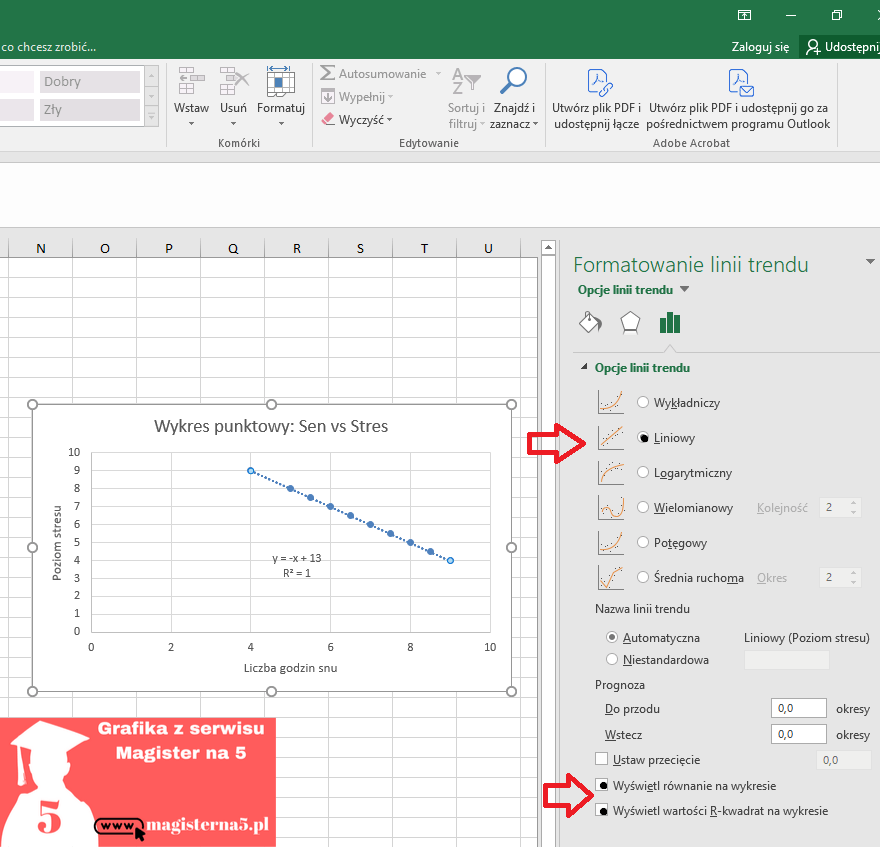
Krok 3 – Dodanie linii trendu z równaniem i R²
- Kliknij na dowolny punkt na wykresie.
- Wybierz Dodaj linię trendu.
- W panelu po prawej zaznacz:
- „Liniowa”
- „Wyświetl równanie na wykresie”
- „Wyświetl wartość R-kwadrat na wykresie”
Teraz na wykresie zobaczysz równanie w formie y = ax + b oraz wartość R², która mówi, jak dobrze linia dopasowuje się do danych (im bliżej 1, tym lepiej).
Krok 4 – Interpretacja regresji liniowej w kontekście pracy magisterskiej
Opis graficzny
Na początku należy krótko opisać, co widać na wykresie:
Na rysunku przedstawiono zależność pomiędzy liczbą godzin snu (oś X) a poziomem stresu (oś Y). Punkty danych układają się w wyraźną linię malejącą, co wskazuje na odwrotną relację między badanymi zmiennymi.
Wyniki modelu
Następnie warto podać wyniki analizy regresji z Excela:
Wyznaczona linia trendu ma równanie: Poziom stresu = –1 × Liczba godzin snu + 13.
Oznacza to, że każdy dodatkowy 1 godzinny przyrost snu wiąże się średnio z obniżeniem poziomu stresu o 1 jednostkę. Wartość współczynnika determinacji R² = 1,00 wskazuje na idealne dopasowanie modelu do danych.
Interpretacja w kontekście badań
Tu przechodzisz od liczb do sensu badania:
Uzyskany wynik sugeruje bardzo silny i negatywny związek pomiędzy liczbą godzin snu a poziomem stresu w badanej próbie. Można stwierdzić, że sen jest istotnym predyktorem poziomu stresu — im więcej snu, tym niższy jego poziom.
Uwagi metodyczne
Warto zaznaczyć ograniczenia, bo recenzenci to lubią:
Idealne dopasowanie modelu (R² = 1) jest w badaniach rzeczywistych zjawiskiem rzadkim. Wynik ten może wynikać z faktu, że analizowany zestaw danych jest przykładowy lub modelowy, a nie z losowo dobranej próby populacyjnej. W badaniach terenowych wartości R² są zazwyczaj niższe, co wynika z większej zmienności i obecności czynników zakłócających.
Zdanie podsumowujące
Analiza potwierdza, że w prezentowanym zbiorze danych liczba godzin snu w pełni wyjaśnia zmienność poziomu stresu, jednak dla pełnej wiarygodności wyników konieczna byłaby weryfikacja na większej i bardziej zróżnicowanej próbie badawczej.
Excel policzy linię trendu i poda równanie, ale nie pokaże od razu p-wartości. Jeśli chcesz mieć pełny raport statystyczny, warto skorzystać z dodatku „Analiza danych” lub Jamovi.
Jak zrobić regresję liniową do pracy magisterskiej w Jamovi – krok po kroku
Zanim zaczniemy klikać w Jamovi, wyobraź sobie, że jesteś na misji: chcesz sprawdzić, czy czas poświęcony na naukę naprawdę przekłada się na lepszy wynik egzaminu. Nie będziemy jednak robić tego „na czuja” ani pytać kolegów z roku, tylko użyjemy do tego twardych danych i narzędzia statystycznego.
W naszym mini-badaniu:
- Zmienna niezależna (X) to czas nauki w godzinach – to, co badany może kontrolować.
- Zmienna zależna (Y) to wynik egzaminu w % – to, co chcemy przewidzieć lub wyjaśnić.
Celem jest sprawdzenie:
Czy więcej godzin nauki faktycznie zwiększa wynik, a jeśli tak – o ile punktów procentowych za każdą dodatkową godzinę?
Regresja liniowa w Jamovi pomoże nam:
- policzyć równanie prostej, które opisuje tę zależność,
- sprawdzić R² – czyli na ile dobrze ta prosta wyjaśnia różnice w wynikach,
- ocenić, czy zależność jest istotna statystycznie (p-wartość),
- i wyciągnąć wnioski, które można elegancko opisać w pracy dyplomowej.
Regresja liniowa w Jamovi instrukcja
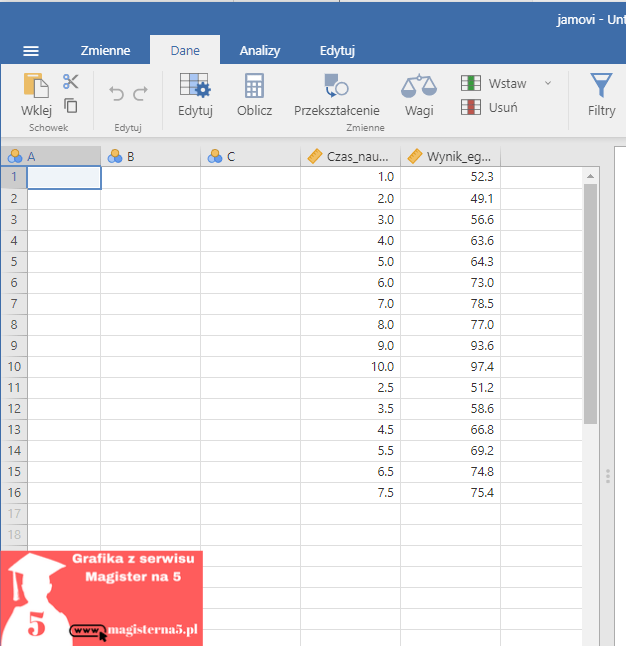
- Stwórz plik np. w excelu z danym np: dane_jamovi_regresja_czas_nauki.xlsx
- W Jamovi wybierz: Dane → Otwórz → Przeglądaj i wskaż pobrany plik.
- W tabeli zobaczysz dwie kolumny:
- Czas_nauki_godz – liczba godzin nauki (X, predyktor)
- Wynik_egzaminu_procent – wynik egzaminu w % (Y, zmienna zależna)[/ms_alert]
Wejdź w: Analizy → Regresja → Regresja liniowa.
Ustaw (za pomocą przeciągnięcia, myszką)
- Zmienna zależna (Dependent Variable) → Wynik_egzaminu_procent
- Współzmienne → Czas_nauki_godz
Następnie ustaw w oknie:
Dopasowanie modelu
- W sekcji Miary dopasowania zaznacz:
- ✅ R – pokazuje współczynnik korelacji
- ✅ R² – mówi, jaka część zmienności zmiennej zależnej jest wyjaśniana przez model
- ✅ Skorygowane R² – uwzględnia liczbę zmiennych w modelu
- W sekcji Ogólny test modelu zaznacz:
- ✅ Test F – sprawdza, czy model jako całość jest istotny statystycznie
- W sekcji Miary dopasowania zaznacz:
Współczynniki modelu
- Rozwiń sekcję Współczynniki modelu i zaznacz:
- ✅ Oszacowanie (Estimate – wartość współczynnika B)
- ✅ Błąd standardowy (Std. Error)
- ✅ t
- ✅ p (p-wartość – istotność statystyczna)
- ✅ 95% przedział ufności
- Weryfikacja założeń
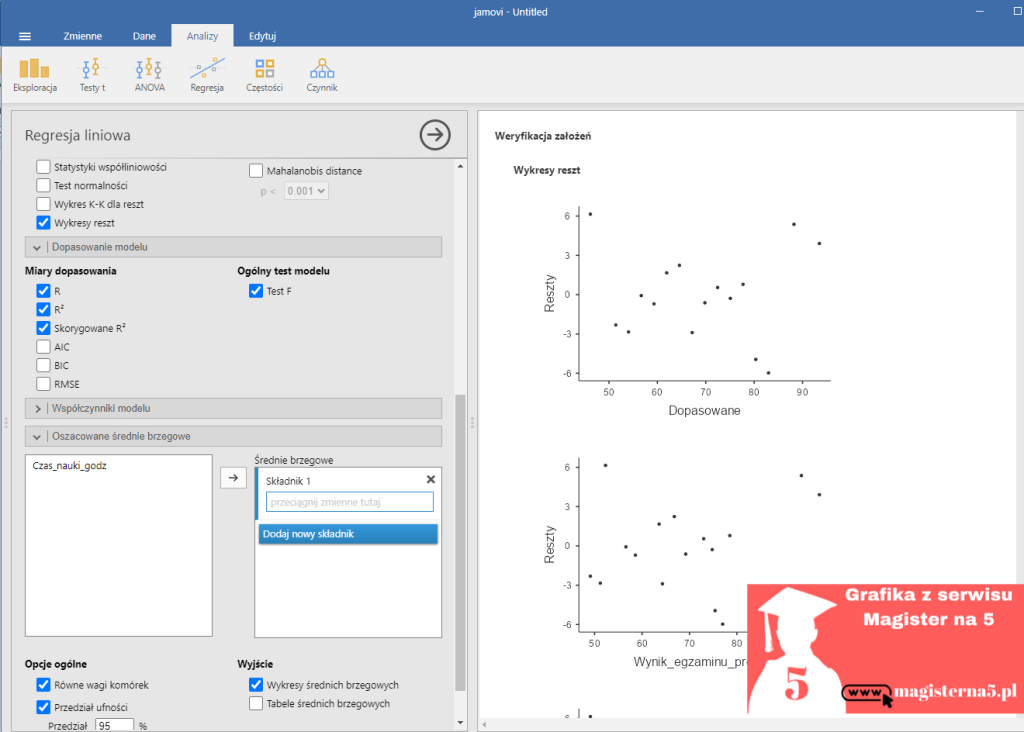
- Zaznacz ✅ Wykresy reszt – pozwalają ocenić, czy reszty są losowo rozproszone wokół 0 (brak wzorca = spełnione założenie homoscedastyczności).
- (Opcjonalnie) Możesz też zaznaczyć Test normalności lub Wykres K-K dla reszt – sprawdzisz wtedy, czy reszty mają rozkład zbliżony do normalnego.
- Rozwiń sekcję Współczynniki modelu i zaznacz:
Opcje ogólne
- Równe wagi komórek – zaznaczone ✅
- Przedział ufności – 95%
💡 Po tych ustawieniach w panelu wyników po prawej stronie powinieneś zobaczyć:
- tabelę z dopasowaniem modelu (R, R², Skorygowane R²),
- Test F z p-wartością,
- tabelę współczynników B z błędami, t, p i przedziałami ufności,
- wykres(y) reszt.
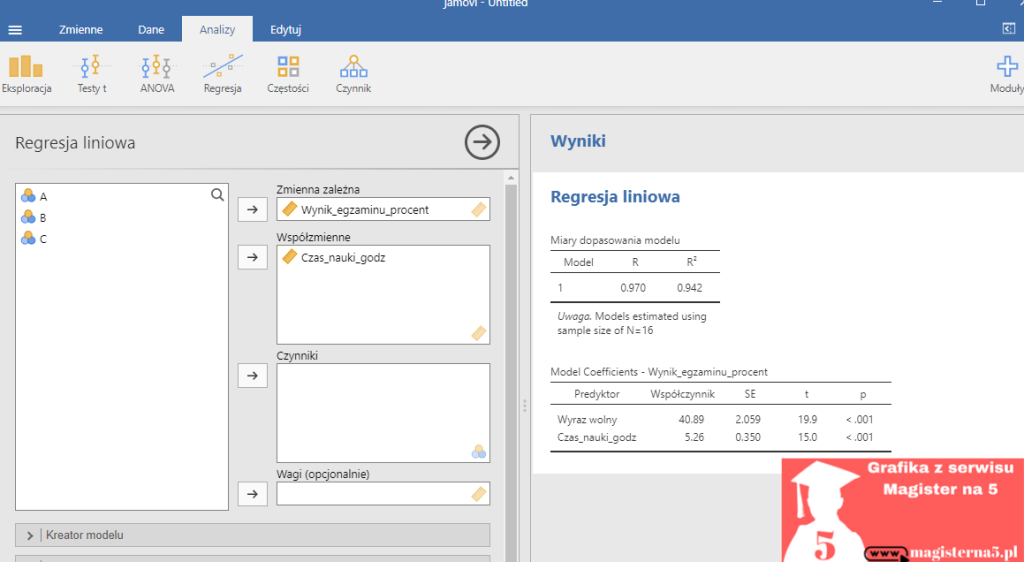
Dokładne wyniki dla tego przykładu wyglądają następująco:
Wszystko to możesz skopiować do swojej pracy i zanalizować, za chwilę powiem jak.
W naszym przypadku, z analizą czasu nauki a wynikiem egzaminu, opis w części „Wyniki”- po prawej stronie może wyglądać tak:
Przeprowadzona analiza regresji liniowej wykazała istotny statystycznie wpływ czasu nauki na wynik egzaminu (B = 5,26; p < 0,001). Model był dobrze dopasowany do danych, wyjaśniając 94% zmienności wyników (R² = 0,94, R² skorygowany = 0,94). Otrzymane równanie regresji: Wynik egzaminu (%) = 40,9 + 5,26 × Czas nauki (godz.). Wzrost czasu nauki o 1 godzinę wiązał się średnio z poprawą wyniku o 5,3 punktu procentowego.
Następnie możesz dodać krótki opis wykresów reszt:
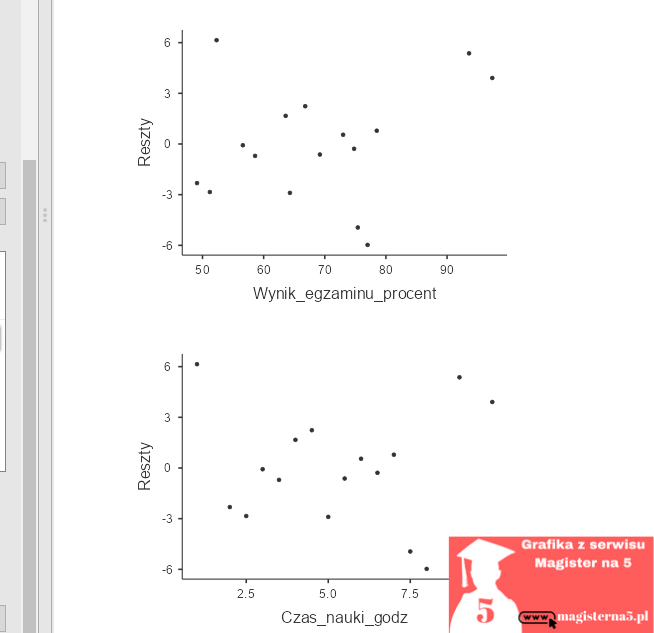
Wykresy reszt potwierdziły prawidłowe dopasowanie modelu. Punkty na wykresie reszt względem wartości dopasowanych były rozmieszczone losowo wokół zera, co wskazuje na brak naruszenia założenia o homoscedastyczności. Wykres QQ wykazał, że reszty mają rozkład zbliżony do normalnego.
Co zrobić z trzema wykresami reszt?
W Jamovi po wykonaniu analizy regresji zwykle pojawiają się:
- Reszty vs Dopasowane – sprawdzasz, czy punkty są równomiernie rozmieszczone wokół 0 (dobrze, jeśli nie tworzą „lejka”).
- Reszty vs Zmienna niezależna – podobna kontrola, ale względem zmiennej X.
- Wykres QQ – punkty powinny leżeć blisko linii prostej (normalność reszt).
W pracy możesz:
- opisać ich interpretację (jak wyżej),
- wkleić wykresy jako ilustracje. Np. „Wykres reszt dla modelu regresji liniowej”
Jak skopiować wykresy regresji liniowej z Jamovi do pracy
- W Jamovi kliknij prawym przyciskiem myszy na wykres → Kopiuj → wklej do Worda (działa jak obraz).
- Możesz też użyć Plik → Eksportuj → PDF/HTML i potem wyciąć wykres z dokumentu.
- Jeśli chcesz mieć je w dobrej jakości, wybierz w Jamovi Zapisz jako obraz (Save as Image) – wtedy dostaniesz plik PNG, który wklejasz bez utraty ostrości.
Jak opisać wyniki regresji liniowej w pracy magisterskiej/licencjackiej
Jak sformułować zdanie z wynikami (język akademicki)
Wyniki regresji zawsze opisujemy w kolejności:
Przykład zapisu:
Analiza regresji liniowej wykazała istotny statystycznie wpływ czasu nauki na wynik egzaminu (B = 5,26; p < 0,001). Model wyjaśniał 94% zmienności wyników egzaminów (R² = 0,94, R² skorygowany = 0,94), co wskazuje na bardzo dobre dopasowanie. Otrzymane równanie regresji: Wynik egzaminu (%) = 40,9 + 5,26 × Czas nauki (godz.).
Jak dodać równanie modelu do tekstu
Równanie możesz wstawić w formie ciągłej lub jako osobny zapis wzorowy.
- Wersja w tekście:
Równanie modelu przyjęło postać: Wynik egzaminu (%) = 40,9 + 5,26 × Czas nauki (godz.).
💡 Warto w przypisie lub nawiasie wyjaśnić, co oznaczają poszczególne elementy równania: wartość stała (wyraz wolny) i współczynnik przy zmiennej.
Jak włączyć wykres do rozdziału badań
- Skopiuj wykres z Jamovi (prawy przycisk myszy → Kopiuj → Wklej do Worda).
- Podpisz go zgodnie z zasadami:
Rys. 5. Wykres punktowy z linią regresji dla zależności między czasem nauki a wynikiem egzaminu.
- W tekście odwołaj się do rysunku:
Na rysunku 5 przedstawiono linię regresji, która obrazuje dodatnią zależność między czasem nauki a wynikiem egzaminu – im więcej czasu przeznaczonego na naukę, tym wyższy wynik procentowy.
W części „Wyniki” opisujesz co wyszło, a w „Dyskusji” dopiero dlaczego tak wyszło i jak to się ma do literatury.
Częste błędy studentów przy stosowaniu regresji
Analiza zbyt małej próby
Regresja liniowa lubi liczby — i to nie tylko w kolumnach, ale też w wielkości próby. Zbyt mała liczba obserwacji powoduje, że wyniki są mało wiarygodne, a model może „widzieć” zależności tam, gdzie tak naprawdę ich nie ma. W praktyce oznacza to ryzyko, że Twój promotor zapyta: „A na ilu badanych to policzyłaś?” i cała magia statystyki pryśnie.
Postaraj się, żeby liczba obserwacji była co najmniej kilkanaście razy większa niż liczba zmiennych w modelu.
Ignorowanie sprawdzenia założeń modelu
Wielu studentów od razu patrzy na R² i p-wartość, ale pomija weryfikację, czy dane w ogóle spełniają podstawowe założenia regresji (np. liniowość, brak silnych wartości odstających, normalność rozkładu reszt, brak heteroskedastyczności).
W Jamovi włącz zawsze „Wykresy reszt” i „Wykres QQ”, a w Excelu sprawdź, czy punkty na wykresie nie układają się w dziwne wzory.
Brak wyjaśnienia, co oznacza R² lub współczynnik B
Samo napisanie „R² = 0,87” nic nie mówi czytelnikowi, jeśli nie dodasz, co to w praktyce znaczy. Podobnie z B — liczba „5,26” wymaga wyjaśnienia, że to np. wzrost wyniku o 5,26 punktu procentowego przy każdej dodatkowej godzinie nauki.
Zawsze interpretuj wynik „po ludzku” — tak, aby ktoś, kto pierwszy raz widzi regresję, mógł zrozumieć jej sens.
Regresja liniowa w pracy magisterskiej podsumowanie
No i proszę – dotarliśmy do końca naszej przygody z regresją liniową, a Ty wiesz już, że to wcale nie jest czarna magia z koszmarów na statystyce, tylko całkiem sprytne narzędzie, które potrafi uratować rozdział badań w pracy dyplomowej. Od prostego wykresu punktowego w Excelu, przez elegancki model w Jamovi, aż po poprawne opisanie wyników – przerobiliśmy cały proces tak, żebyś mogła z dumą pokazać efekty swojemu promotorowi… i żeby ten zapytał: „A to sama Pani policzyła?”, a Ty z pokerową miną przytakniesz.
Wiesz już, kiedy regresja liniowa ma sens, a kiedy lepiej sobie darować, żeby nie wpaść w pułapkę analizowania czegoś, czego się nie da sensownie policzyć. Nauczyłaś się też, że R² to nie tajny kod, tylko prosta informacja, ile z tego, co widzimy w danych, wyjaśnia nasz model – i że nie trzeba rzucać nim w czytelnika bez komentarza. A wykresy reszt? Teraz wiesz, że to nie „dziwne obrazki”, tylko szybki test na to, czy Twoja analiza stoi na solidnym gruncie.
Najważniejsze jednak, że możesz teraz opowiedzieć historię swoich danych – nie suchą, nieodżywioną liczbami, ale taką, która pasuje do Twojego tematu i broni się przed pytaniami komisji. I pamiętaj: jeśli w którymś momencie poczujesz, że Twój model zaczyna żyć własnym życiem i wysyła dziwne sygnały, nie bój się poprosić o wsparcie. Od tego właśnie jest Magister na 5 – żeby pomóc Ci złapać linię trendu nie tylko w danych, ale i w Twojej pracy.
Bo w końcu regresja liniowa to trochę jak dobra rada starszego kolegi: mówi Ci, w którą stronę to wszystko zmierza… ale decyzję, co z tym zrobisz, podejmujesz Ty.
Trochę już wiem o analizie regresji liniowej w pracy magisterskiej. Teraz chcę poznać proces pisania
Naucz się pisać pracę w godzinę. Sprawdź e-book.
Jak napisać pracę w tydzień?
E-book- Jak napisać pracę dyplomową w tydzień? Pobieram teraz>>
Pobieram teraz>>
Dlaczego ten e-book może Ci bardzo pomóc?
- 85 stron samych konkretów- materiał do błyskawicznego wykorzystania.
- Pokaże Ci jak zacząć już za 5 minut. Bez zastanawiania się i marnowania czasu.
- Pokonasz perfekcjonizm i przestaniesz okładać na później.
- Dowiesz się jak pisać pracę 10 razy szybciej, stosując metodę Magistra na 5.
- Uprościliśmy temat, jak tylko się dało. Zrozumiesz, nawet jak nigdy nie pisałeś żadnej pracy.
- Przeczytasz w godzinę. Już nie musisz marnować czasu na dojazdy na uczelnie i seminaria.
- Dostęp w 30 sekund. Materiał dostaniesz w prosto na maila.
- Dostajesz dostęp do wszystkich aktualizacji. Ten produkt to mój absolutny priorytet. Cały czas go ulepszam i dodaje nowe materiały.
- Dużo przykładów. Nie wymyślasz nic od nowa.
- Schematy i wzory działania. Prowadzimy Cię jak po sznurku.
- Dodatkowe ćwiczenia. Zaczniesz działać już na 5 minut.
- Za cenę 4 kaw w Żabce.
Potrzebujesz pomocy z najtrudniejszą częścią swojej pracy?
Metodologia, rozdział badawczy, analiza statystyczna. Błyskawiczna pomoc>>
--
Zobacz opinie:
Zobacz, jakie materiały mogę Ci jeszcze zaproponować.
–>Sklep Magistra na 5
Jeżeli potrzebujesz pomocy, po prostu napisz.
–> Wyślij pytanie


 Przykłady tematów prac magisterskich, w których regresja liniowa ma sens
Przykłady tematów prac magisterskich, w których regresja liniowa ma sens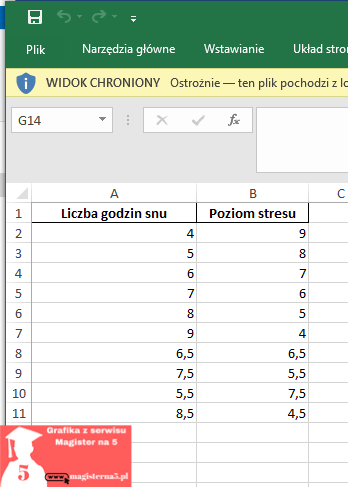


 Pobieram teraz>>
Pobieram teraz>>




