Ostatnia aktualizacja 13 października 2025
„Kwartyle” brzmią jak nazwy domów w Hogwarcie, a to po prostu sprytny sposób, żeby zobaczyć, co dzieje się w środku Twoich danych – bez dawania się nabrać średniej. Średnia potrafi ładnie kłamać (jeden „geniusz” z 100 pkt i już cała grupa wygląda super). Kwartyle mówią: ile ma „dół” (Q1), gdzie jest środek (mediana), a jak wygląda „góra” (Q3). Do tego dochodzi IQR – rozstęp między Q1 i Q3 – czyli „jak szeroka jest paczka środkowych 50% wyników”.
Po co Ci to w pracy dyplomowej? Bo promotor nie chce tylko jednej liczby. Chce wiedzieć, czy Twoje wyniki są spójne, czy może masz skrajności, i jak różnią się grupy. Kwartyle i IQR to szybka mapa: pokazują realny obraz – bez szumu i bez „dziwaków”.
W tym artykule ogarniemy: co to są kwartyle, kiedy je stosować (a kiedy lepiej nie), jakie mają plusy i minusy, jak je policzyć w Excelu, i jak ładnie opisać to w pracy. Będzie prosto, krótko i z przykładami. Jedziemy! 🚀📊
Potrzebujesz szybkiej pomocy z obliczeniem kwartyli w swojej pracy dyplomowej? Kliknij poniżej
–> Kwartyle w pracy magisterskiej. Błyskawiczna pomoc
–> Wzory rozdziałów badawczych ze statystyką
Nie wiem, jak zacząć. Masz coś dla mnie?
–> E-book- Jak Napisać Pracę Dyplomową W Tydzień
–> Pobierz przykładową pracę licencjacką
Co to kwartyle? Definicja łatwa do ogarnięcia
Kwartyle dzielą Twoje posortowane dane na cztery równe części.
Myśl o nich jak o „znacznikach” na drodze wyników:
- Q1 (pierwszy kwartyl) – punkt, poniżej którego leży ok. 25% danych (czyli „dół”).
- Mediana (Q2) – środek: połowa wartości jest niżej, połowa wyżej (50%/50%).
- Q3 (trzeci kwartyl) – punkt, poniżej którego leży ok. 75% danych (czyli „góra środka”).
Z tego bierzemy jeszcze IQR (InterQuartile Range):
IQR = Q3 − Q1 → szerokość „środkowej paczki” 50% wyników (od Q1 do Q3).
IQR jest odporny na „dziwaków” (pojedyncze skrajne wartości).
Mini-przykład
Dane (posortowane): 55, 60, 68, 70, 74, 78, 82, 85, 90
- Q1 ≈ 68 • Mediana = 74 • Q3 ≈ 85
- IQR = 85 − 68 = 17 (środkowe 50% wyników mieści się w przedziale 68–85)
Jedno zdanie do zapamiętania:
Kwartyle pokazują, gdzie jest dół (Q1), środek (mediana) i góra (Q3) Twoich danych, a IQR mówi, jak szeroko rozlała się ta środkowa połowa.
Po co kwartyle w pracy dyplomowej?
Wyobraź sobie, że patrzysz na wyniki kolosa. Średnia wyszła 75. Brzmi okej… tylko czy to znaczy, że wszyscy mieli okolice 75? A może połowa ma 90+, a druga połowa ledwo dociągnęła do 60? Tu właśnie wjeżdżają kwartyle – Twoi „tajni informatorzy” o tym, co dzieje się w środku danych.
- Q1 to „dół” (25% najsłabszych wyników).
- Mediana to środek (połowa niżej, połowa wyżej).
- Q3 to „górka” (75% wyników jest poniżej).
A IQR = Q3 – Q1 to szerokość „paczki” środkowych 50% wyników. Innymi słowy: jak bardzo rozjechana jest typowa część grupy – bez skrajnych odpałów.
Po co Ci kwartyle w rozdziale badawczym?
Bo średnia potrafi ściemniać. Jedna osoba z 100 punktami i cyk — wszyscy „wyglądają” świetnie. Kwartyle mówią: „spokojnie, połowa ludzi ma między Q1 a Q3, czyli np. 68–82”. Nagle widzisz prawdziwy obraz: gdzie leży środek i jak szeroko rozlane są typowe wyniki. Promotor to kocha, bo to opis uczciwy i odporny na dziwaków (outliery).
Przykład
Masz dwie grupy:
- Grupa A: mediana 70 (Q1–Q3: 65–78)
- Grupa B: mediana 75 (Q1–Q3: 69–83)
Co mówisz? „B ma trochę wyższy środek, ale rozrzut typowych wyników podobny.” Bez filozofii, zrozumiale dla każdego.
Gdzie kwartyle możesz wstawić do pracy dyplomowej?
- W statystykach opisowych: zamiast samej średniej napisz mediana (Q1–Q3) i IQR.
- Przy porównaniu grup: podaj mediany i zakresy Q1–Q3 — od razu widać różnice.
- Przy outlierach: reguła 1,5×IQR pozwala grzecznie wskazać „bardzo podejrzane” punkty.
Gotowce do wklejenia:
- „Ze względu na skośny rozkład raportowano medianę oraz kwartyle (Q1–Q3); IQR opisuje rozrzut środkowych 50% wyników.”
- „Grupa A: 70 (65–78) vs Grupa B: 75 (69–83) — B ma wyższy poziom centralny przy podobnym rozrzucie.”
- „Wartości odstające zidentyfikowano regułą 1,5×IQR.”
Podsumowując, kwartyle to statystyczna wersja „sprawdź, co w środku, zanim ocenisz po okładce”. Średnia robi PR, kwartyle robią real talk. 📦📊😉
Kiedy stosować kwartyle, a kiedy nie
Kwartyle mówią, co dzieje się w środku danych (Q1–Mediana–Q3), a IQR (Q3−Q1) pokazuje, jak szeroko rozlana jest „typowa połowa”. Świetne, gdy średnia ściemnia.
✅ Stosuj, gdy:
- Masz rozkład skośny albo widzisz „dziwaki” (outliery).
Przykład: czasy dojazdu na uczelnię – jeden mieszka naprzeciwko, ktoś inny dojeżdża 2 h. - Skale porządkowe (Likert 1–5) lub dane, które nie spełniają założeń normalności.
Przykład: „zgadzam się / nie zgadzam się” – tu mediana i kwartyle lepsze niż średnia. - Chcesz uczciwego opisu środka i „typowego” rozrzutu (IQR), a nie numeru zepsutego przez ekstremalne wartości.
- Porównujesz grupy nieparametrycznie (często z testami Manna–Whitneya/Kruskala–Wallisa) i pokazujesz mediana (Q1–Q3).
- Robisz boxploty – kwartyle i IQR to ich serce.
❌ Nie stosuj (albo nie tylko tego), gdy:
- Dane są kategoryczne bez porządku (kierunek studiów, płeć).
Tu używaj częstości i procentów, nie kwartylów. - Potrzebujesz miar do modeli parametrycznych, gdzie używa się średniej i SD (np. klasyczna regresja liniowa – opisowo podaj oba: medianę/Q1–Q3 i średnią/SD).
- Masz bardzo małą próbę (np. n=5) – kwartyle istnieją, ale są mało stabilne; pokaż też surowe wartości/wykres.
- Chcesz pełnej informacji o skrajnościach – IQR ignoruje brzegi; wtedy pokaż dodatkowo min–max/rozstęp.
⚠️ Typowe wpadki
- Mylisz IQR z rozstępem (MAX−MIN).
Fix: IQR to tylko środkowe 50% (Q1–Q3). - Raportujesz tylko średnią przy skośnych danych.
Fix: dodaj medianę i Q1–Q3 (i/lub IQR). - Używasz kwartylów dla czystych kategorii.
Fix: dla kategorii – tylko liczności/procenty. - Zapominasz o outlierach.
Fix: wspomnij regułę 1,5×IQR i pokaż, co zrobiłeś z obserwacjami skrajnymi.
Jedno zdanie do zapamiętania
Kwartyle i IQR włączaj, gdy chcesz „real talk” o środku i typowym rozrzucie, średnią i SD – gdy rozkład jest grzeczny i (prawie) normalny. Po prostu dobierz narzędzie do kształtu danych.
Przykłady tematów i kierunków studiów, w których można zastosować kwartyle
🎓 Pedagogika / Edukacja
Temat: Wyniki testu z matematyki w klasie A vs B.
Co zbierasz: punkty z testu (liczby).
Jak użyć kwartylów: policz medianę i Q1–Q3 dla każdej klasy; IQR porówna „typowy rozrzut”.
Co to pokaże:
- która klasa ma typowo wyższe wyniki (mediana),
- czy wyniki są równe czy rozjechane (IQR)
Zdanie do pracy:
„Klasa A: mediana 70 (Q1–Q3: 65–78), IQR = 13; Klasa B: 75 (69–83), IQR = 14 — klasa B ma wyższy poziom centralny przy podobnym rozrzucie typowych wyników.”
🧠 Psychologia
Temat: Stres studentów przed i po sesji.
Co zbierasz: skala stresu 1–10.
Jak użyć kwartylów: dla „przed” i „po” podaj medianę (Q1–Q3) i IQR.
Co to pokaże:
- czy typowy stres spadł (zmiana mediany),
- czy grupa stała się bardziej równa (mniejszy IQR).
Zdanie do pracy:
„Przed sesją: 7 (6–8), IQR=2; po sesji: 5 (4–6), IQR=2 — mediana stresu spadła o 2 punkty, rozrzut typowych wyników pozostał stabilny.”
🩺 Pielęgniarstwo / Zdrowie publiczne / Dietetyka
Temat: Czas rehabilitacji po zabiegu – program interwencyjny vs kontrola.
Co zbierasz: dni rehabilitacji.
Jak użyć kwartylów: mediana (Q1–Q3) i IQR dla obu grup; outliery sprawdź regułą 1,5×IQR.
Co to pokaże:
- „typowy” czas rehabilitacji w każdej grupie,
- czy program skraca i stabilizuje rehabilitację (niższa mediana i mniejszy IQR).
Zdanie do pracy:
„Interwencja: 12 dni (10–15), IQR=5; kontrola: 16 (12–21), IQR=9 — program skraca typowy czas i zmniejsza zróżnicowanie.”
👔 Zarządzanie / HR
Temat: Satysfakcja z pracy w działach (skala Likert 1–5).
Co zbierasz: odpowiedzi 1–5.
Jak użyć kwartylów: raportuj medianę i Q1–Q3; IQR pokaże spójność nastrojów.
Co to pokaże:
- który dział ma typowo wyższą satysfakcję,
- czy zadowolenie jest stabilne (mały IQR) czy podzielone (duży IQR).
Zdanie do pracy:
„Dział X: 4 (3–4), IQR=1; Dział Y: 3 (2–4), IQR=2 — X ma wyższą medianę i bardziej jednorodne odpowiedzi.”
💼 Ekonomia / Marketing
Temat: Wartość koszyka zakupowego w kampanii A vs B.
Co zbierasz: zł na zamówienie (skośne dane).
Jak użyć kwartylów: mediana (Q1–Q3) i IQR zamiast samej średniej (odporność na drogie „odpały”).
Co to pokaże:
- ile typowo wydaje klient w każdej kampanii,
- czy kampania daje stabilniejsze koszyki (IQR).
Zdanie do pracy:
„A: 82 zł (60–110), IQR=50; B: 95 (70–130), IQR=60 — kampania B typowo wyższy koszyk, lecz większa zmienność.”
💻 Informatyka
Temat: Czas wykonania zadania w interfejsie A/B.
Co zbierasz: sekundy/minuty.
Jak użyć kwartylów: mediana (Q1–Q3) i IQR na grupę; boxploty.
Co to pokaże:
- który interfejs jest typowo szybszy (niższa mediana),
- stabilność doświadczenia (mniejszy IQR = równe czasy).
Zdanie do pracy:
„A: 58 s (45–72), IQR=27; B: 46 s (38–55), IQR=17 — B szybszy i bardziej przewidywalny.”
🌿Ochrona Środowiska
Temat: Stężenie PM2.5 w dzielnicach.
Co zbierasz: µg/m³, pomiary dzienne.
Jak użyć kwartylów: mediana (Q1–Q3) i IQR per dzielnica; outliery (1,5×IQR).
Co to pokaże:
- „typowy” poziom smogu (nie psuty przez piki),
- która dzielnica ma stabilniejsze powietrze.
Zdanie do pracy:
„Centrum: 28 (19–41), IQR=22; Obrzeża: 17 (12–24), IQR=12 — centrum typowo wyższe i bardziej zmienne stężenia.”
🏗️ Inżynieria / Logistyka
Temat: Czas dostawy u trzech przewoźników.
Co zbierasz: dni/godziny dostawy.
Jak użyć kwartylów: dla każdego przewoźnika policz medianę (Q1–Q3) i IQR.
Co to pokaże:
- kto dostarcza typowo szybciej,
- kto jest stabilniejszy (mniejszy IQR).
Zdanie do pracy:
„P1: 2,1 dnia (1,8–2,6), IQR=0,8; P2: 2,9 (2,2–4,1), IQR=1,9 — P1 szybszy i bardziej przewidywalny.”
⚖️ Socjologia / Administracja
Temat: Dochody gospodarstw domowych w dwóch regionach.
Co zbierasz: zł/mies. (rozkład skośny).
Jak użyć kwartylów: mediana (Q1–Q3) i IQR zamiast samej średniej.
Co to pokaże:
- dochód typowy (połowa gospodarstw),
- nierówność w obrębie regionu (IQR).
Zdanie do pracy:
„Region A: 3 800 (3 000–4 600), IQR=1 600; Region B: 4 300 (3 300–5 300), IQR=2 000 — B wyższa mediana, ale większe zróżnicowanie.”
🏃♀️ Sport / Fizjoterapia
Temat: Czas biegu 5 km – plan treningowy 1 vs 2.
Co zbierasz: min:s.
Jak użyć kwartylów: mediana (Q1–Q3) i IQR per plan; boxplot.
Co to pokaże:
- który plan daje typowo lepszy czas,który jest równiejszy (IQR).
Zdanie do pracy:
„Plan 1: 25:10 (23:40–27:05), IQR=3:25; Plan 2: 23:45 (22:30–25:00), IQR=2:30 — Plan 2 szybszy i bardziej spójny.”
📣 Komunikacja / Media
Temat: Czas czytania artykułu w wersji krótkiej vs długiej.
Co zbierasz: sekundy.
Jak użyć kwartylów: mediana (Q1–Q3) i IQR; porównaj formaty.
Co to pokaże:
- realny typowy czas czytania,
- czy krótsza wersja jest stabilniej konsumowana.
Zdanie do pracy:
„Krótka: 46 s (35–58), IQR=23; Długa: 71 s (53–95), IQR=42 — krótka czytana szybciej i bardziej równomiernie.”
Jak policzyć kwartyle w Excelu?
W Excelu otwórz pusty arkusz, kliknij komórkę A1 i wklej swoje dane. Ja mam przykładowe 20 wyników.
Co wpisujesz krok po kroku?
- Kliknij komórkę, gdzie ma się pojawić wynik, np. D2.
- Wpisz:
- =KWARTYL.PRZEDZ.OTW(B2:B21;1)
👉 To da Ci pierwszy kwartyl (Q1).
- Wpisz w kolejne komórki:
- Mediana (Q2):
- =KWARTYL.PRZEDZ.OTW(B2:B21;2)
- Trzeci kwartyl (Q3):
- =KWARTYL.PRZEDZ.OTW(B2:B21;3)
- Rozstęp międzykwartylowy (IQR):
=KWARTYL.PRZEDZ.OTW(B2:B21;3)-KWARTYL.PRZEDZ.OTW(B2:B21;1)
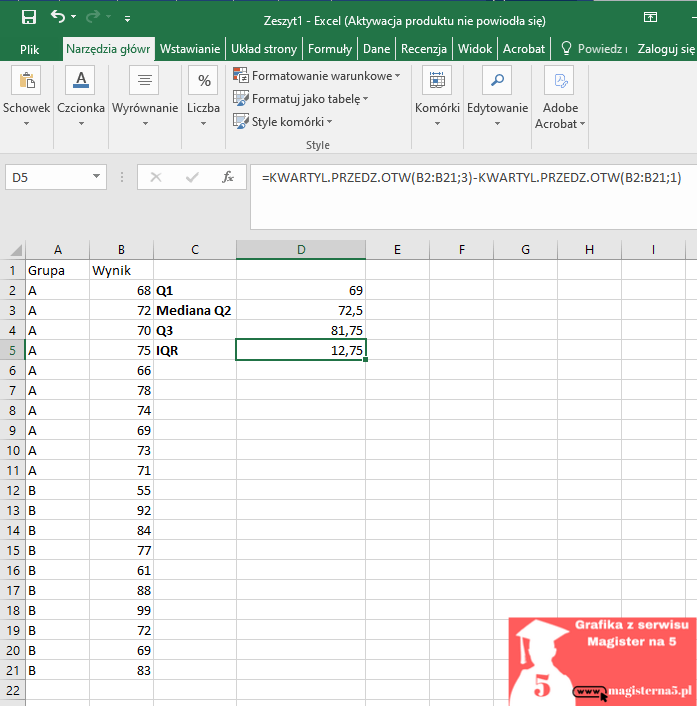
Spójrz, jak to wygląda na moim przykładzie:
Jak zinterpretować kwartyle w Excelu ?
Mediana 72,5 → „typowy” wynik to ok. 72–73 pkt (połowa osób ma mniej, połowa więcej).
- Q1–Q3 = 69–81,75 → środkowe 50% badanych mieści się między 69 a 81,75 pkt.
Innymi słowy: większość wyników krąży w przedziale szerokości 12,75 pkt. - IQR = 12,75 → tyle wynosi „rozrzut typowych wyników”. To umiarkowana zmienność – nie idealnie równo, ale bez wielkiego chaosu.
(Dodatkowo) Outliery wg reguły 1,5×IQR
- Dolna granica: Q1 − 1,5·IQR = 69 − 19,125 = 49,88
- Górna granica: Q3 + 1,5·IQR = 81,75 + 19,125 = 100,88
Jeśli Twoje dane mieszczą się w tych granicach (np. min 55, max 99), nie ma podejrzenia wartości odstających.
Gotowy opis do pracy
„Z uwagi na skośność danych przedstawiono miary odporne. Mediana wyniosła 72,5, natomiast kwartyle Q1–Q3 = 69–81,75, co daje rozstęp międzykwartylowy (IQR) = 12,75. Oznacza to, że środkowe 50% obserwacji mieści się w przedziale 69–81,75 pkt, a zróżnicowanie typowych wyników jest umiarkowane. Zgodnie z regułą 1,5×IQR (granice: 49,88–100,88) w zbiorze nie zidentyfikowano wartości odstających.”
Wersja krótka (np. do tabeli/legendy wykresu)
Mediana 72,5; Q1–Q3: 69–81,75; IQR: 12,75. Środkowe 50% wyników w przedziale 69–81,75; brak outlierów (1,5×IQR).
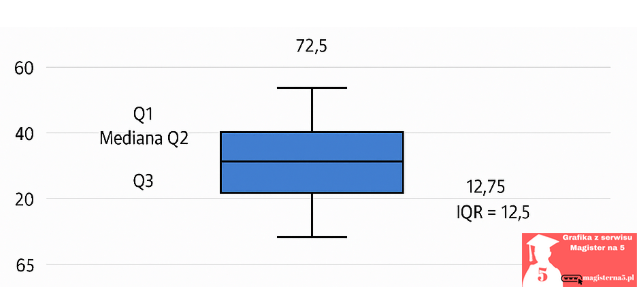
Na poniższym wykresie pudełkowym przedstawiono rozkład wyników badanych, z uwzględnieniem mediany, kwartylów oraz rozstępu międzykwartylowego (IQR).
Mediana wyniosła 72,5 punktu, co oznacza, że połowa badanych uzyskała wynik niższy, a połowa wyższy. Większość wyników (środkowe 50%) mieści się między 69 a 81,75 punktu, co wskazuje na umiarkowane zróżnicowanie danych. Brak wartości odstających sugeruje, że badana grupa była dość jednorodna pod względem osiąganych wyników.
Najczęstsze błędy studentów przy kwartylach
Mylenie IQR z rozstępem (MAX–MIN)
❌ Błąd: „IQR to różnica między największą a najmniejszą wartością.”
✅ Poprawnie: IQR = Q3 − Q1, czyli rozstęp środkowych 50% wyników.
Podawanie tylko średniej przy skośnych danych
❌ Błąd: raportowanie wyłącznie średniej i odchylenia standardowego.
✅ Lepiej: przy danych skośnych pokaż medianę, kwartyle (Q1–Q3) i IQR – dają pełniejszy, uczciwszy obraz.
Złe funkcje w Excelu
❌ Błąd: użycie starego KWARTYL lub KWARTYL.PRZEDZ.ZAMK.
✅ Poprawnie: korzystaj z KWARTYL.PRZEDZ.OTW(zakres;1/2/3) – to aktualna i zgodna z nowszymi programami wersja.
Brak jednostek lub kontekstu
❌ Błąd: podanie suchych liczb – „Q1 = 69, IQR = 12,75” – bez wyjaśnienia.
✅ Poprawnie: dodaj jednostki i komentarz, np. „Środkowe 50% wyników mieści się między 69 a 81,75 pkt.”
Ignorowanie wartości odstających (outlierów)
❌ Błąd: brak wzmianki o skrajnych wartościach.
✅ Poprawnie: sprawdź regułę 1,5×IQR (Q1−1,5×IQR i Q3+1,5×IQR) i napisz, czy znaleziono obserwacje odstające.
Liczenie kwartylów dla danych kategorycznych
❌ Błąd: próba obliczenia kwartylów dla „płci” czy „kierunku studiów”.
✅ Poprawnie: kwartyle stosuje się tylko do danych liczbowych lub porządkowych (np. skale 1–5).
Wyciąganie wniosków bez testu statystycznego
❌ Błąd: „Mediana w grupie A jest wyższa, więc jest różnica.”
✅ Poprawnie: do potwierdzenia różnic użyj testu Manna–Whitneya lub Kruskal–Wallisa i podaj wartość p.
Zbyt mocne zaokrąglanie wyników
❌ Błąd: 72,53 → 73; 12,75 → 13.
✅ Poprawnie: zostaw dwa miejsca po przecinku, by zachować precyzję.
Niepodanie źródła metody obliczeń
❌ Błąd: brak informacji, jak liczono kwartyle.
✅ Poprawnie: w metodologii napisz np.:
„Kwartyle obliczono w programie Microsoft Excel za pomocą funkcji KWARTYL.PRZEDZ.OTW.”
Mieszanie danych z różnych grup
❌ Błąd: obliczanie kwartylów dla całej próby zamiast osobno dla grup A i B.
✅ Poprawnie: używaj filtrów lub funkcji FILTROWANIE (Excel 365) / JEŻELI (starsze wersje).
Zbyt mała próba i zbyt odważne wnioski
❌ Błąd: wyciąganie silnych wniosków przy małej liczbie danych (np. n=6).
✅ Poprawnie: pokaż kwartyle, ale napisz ostrożnie: „Wnioski należy interpretować z uwagi na małą liczebność próby.”
Brak spójności między miarami
❌ Błąd: raz pokazujesz średnią i SD, raz medianę i IQR – bez uzasadnienia.
✅ Poprawnie: wybierz jeden zestaw miar i trzymaj się go w całej analizie (np. medianę i IQR przy danych skośnych).
Kwartyle w pracy magisterskiej zakończenie
I tyle. Kwartyle przestały być tajemniczym zaklęciem z podręcznika i okazały się… bardzo praktyczną mapą danych. Q1 mówi, gdzie zaczyna się „typowa paczka”, mediana pokazuje środek, Q3 – jej górny brzeg, a IQR mówi, jak szeroka jest ta paczka. Zero magii, czysta logika.
Po co Ci to w dyplomie? Bo średnia lubi robić PR, a kwartyle robią real talk: pokazują, jak ma większość badanych, a nie jeden rekordzista. Dzięki nim napiszesz zdanie, które brzmi mądrze i jest prawdziwe: „Środkowe 50% wyników mieści się między… a…, a typowy wynik to…” — i już recenzent widzi, że wiesz, co robisz.
Zapamiętaj prosty schemat:
- Podaj liczby: napisz medianę (typowy wynik) oraz Q1–Q3 (zakres większości wyników) i IQR (szerokość tej większości). Dodaj jednostki: pkt, min, zł.
- Pokaż obrazek: zrób wykres pudełkowy (boxplot) – widać środek i rozrzut na pierwszy rzut oka.
- Sprawdź skrajności: policz granice 1,5 × IQR i zobacz, czy są odstające wartości (bardzo niskie albo bardzo wysokie).
- Napisz po ludzku jedno zdanie: co to znaczy dla Twoich danych.
A jeśli ktoś zapyta, czym są kwartyle, możesz z uśmiechem odpowiedzieć:
„To sposób, żeby zobaczyć, co dzieje się w środku danych — zanim znowu damy się nabrać średniej.” 📦📊😉
Trochę już wiem o kwartylach w pracy magisterskiej. Teraz chcę poznać proces pisania
Naucz się pisać pracę w godzinę. Sprawdź e-book.
Jak napisać pracę w tydzień?
E-book- Jak napisać pracę dyplomową w tydzień? Pobieram teraz>>
Pobieram teraz>>
Dlaczego ten e-book może Ci bardzo pomóc?
- 85 stron samych konkretów- materiał do błyskawicznego wykorzystania.
- Pokaże Ci jak zacząć już za 5 minut. Bez zastanawiania się i marnowania czasu.
- Pokonasz perfekcjonizm i przestaniesz okładać na później.
- Dowiesz się jak pisać pracę 10 razy szybciej, stosując metodę Magistra na 5.
- Uprościliśmy temat, jak tylko się dało. Zrozumiesz, nawet jak nigdy nie pisałeś żadnej pracy.
- Przeczytasz w godzinę. Już nie musisz marnować czasu na dojazdy na uczelnie i seminaria.
- Dostęp w 30 sekund. Materiał dostaniesz w prosto na maila.
- Dostajesz dostęp do wszystkich aktualizacji. Ten produkt to mój absolutny priorytet. Cały czas go ulepszam i dodaje nowe materiały.
- Dużo przykładów. Nie wymyślasz nic od nowa.
- Schematy i wzory działania. Prowadzimy Cię jak po sznurku.
- Dodatkowe ćwiczenia. Zaczniesz działać już na 5 minut.
- Za cenę 4 kaw w Żabce.
Potrzebujesz pomocy z najtrudniejszą częścią swojej pracy?
Metodologia, rozdział badawczy, analiza statystyczna. Błyskawiczna pomoc>>
--
Zobacz opinie:
Zobacz, jakie materiały mogę Ci jeszcze zaproponować.
–>Sklep Magistra na 5
Jeżeli potrzebujesz pomocy, po prostu napisz.
–> Wyślij pytanie



 Pobieram teraz>>
Pobieram teraz>>




