Ostatnia aktualizacja 24 września 2025
Promotor pyta: „a sprawdziła/łeś równość wariancji?” i masz minę jak 🤔? Spokojnie. To tylko pytanie, czy grupy rozrzucają się podobnie (czy wyniki w A „falują” tak samo jak w B).
W tym krótkim tekście dowiesz się po co Ci to w pracy dyplomowej, co dokładnie znaczy homogeniczność wariancji, jak to sprawdzić w prosty sposób (na oko i testem), oraz co zrobić, gdy warunek nie trzyma (spokojnie, są gotowe alternatywy). Dorzucam też gotowe zdania do wklejenia i szybkie przykłady z różnych kierunków. Pięć minut i masz temat ogarnięty.
Potrzebujesz szybkiej pomocy z obliczeniem homogeniczności wariancji w pracy dyplomowej? Kliknij poniżej
–> Homogeniczność wariancji do pracy magisterskiej. Błyskawiczna pomoc
–> Wzory rozdziałów badawczych ze statystyką
Nie wiem, jak zacząć. Masz coś dla mnie?
–> E-book- Jak Napisać Pracę Dyplomową W Tydzień
–> Pobierz przykładową pracę licencjacką

Homogeniczność wariancji, o co tu chodzi? Co znaczy „równy rozrzut” między grupami?
Homogeniczność wariancji (zw. też równością wariancji albo homoscedastycznością) to po prostu sytuacja, w której porównywane grupy mają podobny rozrzut wyników.
Rozrzut = jak bardzo wyniki się „rozsypują” wokół średniej (czyli czy są do siebie zbliżone, czy latają od nisko do bardzo wysoko).
- Jeśli w grupie A i grupie B wyniki „falują” podobnie (np. w obu odchylenie standardowe jest ~10 punktów), to mówimy, że wariancje są homogeniczne.
- Nie chodzi o to, żeby były identyczne co do przecinka – wystarczy zbliżone.
Mini-przykład:
- Grupa A: średnia 70, typowe odchylenie ok. 10.
- Grupa B: średnia 85, typowe odchylenie ok. 11.
Średnie są inne (70 vs 85), ale rozrzut podobny (10 vs 11) → wariancje można uznać za z grubsza równe.
Nie myl z równością średnich. Homogeniczność mówi o szerokości chmury punktów, a nie o tym, gdzie ta chmura leży. Możesz mieć inne średnie, a jednocześnie podobny rozrzut – i właśnie to lubią klasyczne testy porównujące średnie (np. t-test, ANOVA).
Po co Ci homogeniczność wariancji w pracy magisterskiej?
Bo od równości (podobieństwa) rozrzutów zależy, czy wolno Ci użyć „klasycznych” porównań średnich, i czy wnioski będą wiarygodne.
- Dobór właściwego testu. Gdy rozrzuty są podobne, możesz użyć standardowej wersji testu t lub analizy wariancji (ANOVA). Gdy nie są podobne, wybierasz wersję Welcha (działa bez tego założenia). Dzięki temu nie „przekręcasz” wyników.
- Uczciwe wnioski. Nierówne rozrzuty potrafią zawyżyć albo zaniżyć „istotność” różnic między grupami. Sprawdzenie tego warunku to hamulec bezpieczeństwa przed błędną interpretacją.
- Szacunek promotora i spokojna obrona. Pokazujesz, że kontrolujesz założenia testów, a nie tylko wklejasz liczby.
- Lepszy opis „Metod”. Możesz napisać wprost, co sprawdziłaś/eś i dlaczego użyłaś/eś danej wersji testu.
- Porównywalność grup. Jeśli jedna grupa ma „mega rozsypkę”, a druga „ciasno”, porównanie samych średnich bywa mylące — to właśnie wyłapuje test na homogeniczność.
Gotowe zdanie do wklejenia:
„Przed porównaniem średnich sprawdzono homogeniczność wariancji (równość rozrzutów między grupami) testem Levene’a; w przypadku naruszenia zastosowano test t w wersji Welcha (odporny na nierówne wariancje).”
Kiedy homogeniczność wariancji ma znaczenie?
Zawsze wtedy, gdy porównujesz średnie albo budujesz prosty model przewidywania. Chodzi o to, by grupy (albo błędy w modelu) miały podobny rozrzut. Jeśli rozrzuty są bardzo różne, klasyczne metody potrafią „krzywo” ocenić różnice.
a) t-test (dwie grupy, np. kobiety vs mężczyźni)
Cel: sprawdzić, czy średnie w dwóch grupach się różnią.
Założenie: podobny rozrzut w obu grupach.
Co robisz: rzuć okiem na odchylenia standardowe i zrób test Levene’a.
Jeśli rozrzuty nierówne → użyj t-testu Welcha (ten nie wymaga równości wariancji).
b) ANOVA (trzy i więcej grup, np. trzy kierunki studiów)
Cel: sprawdzić, czy przynajmniej jedna średnia różni się od pozostałych.
Założenie: podobny rozrzut w każdej z grup.
Co robisz: Levene/Brown–Forsythe przed analizą.
Jeśli nierówne → ANOVA Welcha albo prosty „plan B”: testy nieparametryczne (np. Kruskal–Wallis).
c) Prosta regresja (np. czas zadania ~ staż w aplikacji)
Cel: sprawdzić, czy zmienna X pomaga przewidzieć Y.
Założenie (tu mówi się „homoscedastyczność”): rozrzut błędów modelu powinien być podobny dla małych i dużych wartości przewidywanych.
Co robisz: po dopasowaniu modelu zerkasz na wykres reszt vs wartości przewidywane — chmura punktów powinna mieć zbliżoną „szerokość”.
Jeśli „lejek” (małe błędy dla małych wartości, duże dla dużych) → rozważ transformację (np. logarytm z Y) albo regresję odporną.
Krótko:
- Porówniasz średnie → sprawdź równość rozrzutu (Levene) i w razie czego bierz Welcha.
- Budujesz regresję → sprawdź, czy błędy mają podobny rozrzut; jeśli nie, użyj transformacji lub metod odpornych.
Dzięki temu Twoje wnioski są uczciwe i stabilne: nie „wychodzą” tylko dlatego, że jedna grupa ma dużo większą „rozsypkę” niż druga.
Jak sprawdzić homogeniczność wariancji w pracy magisterskiej?
Szybki rzut oka. Zaczynasz od podglądu danych. Najprościej narysuj wykres pudełkowy dla każdej grupy i porównaj wysokość pudełek oraz „wąsów”. Jeśli są do siebie podobne, rozrzut też jest podobny.
Gdy jedno pudełko jest wyraźnie wyższe/szersze od innych, ta grupa ma większą zmienność i może być problem z równością. Dla pewności policz w każdej grupie odchylenie standardowe: jeśli największe nie jest większe niż około dwa razy najmniejsze, zwykle możesz śmiało iść w klasyczne porównania średnich.
Spójrz na przykład:
Jak czytać? w pierwszym obrazku pudełka i „wąsy” są podobnej wysokości → rozrzut podobny (OK do klasycznych testów). W drugim pudełko dla Grupy B jest dużo „wyższe/szersze” → rozrzut większy, lepiej użyć Welcha albo rozważyć transformację/testy nieparametryczne.
Test formalny. Gdy „na oko” wygląda ok (albo gdy chcesz mieć twardy dowód), robisz test Levene’a. On odpowiada na pytanie: czy rozrzuty w grupach są do siebie zbliżone.
Odczyt jest banalny: p ≥ 0,05 – brak dowodów na różne wariancje, działasz dalej jak zwykle; p < 0,05 – wariancje się różnią, trzeba zmienić plan. Jeśli masz sporo wartości skrajnych lub skośny rozkład, jeszcze lepszy będzie Brown–Forsythe (to „odporniejszy” kuzyn Levene’a). Bartlett jest ok, ale tylko wtedy, gdy dane są naprawdę bliskie normalnym – inaczej bywa przewrażliwiony.
Jak sprawdzić homogeniczność wariancji w Jamovi (na przykładzie)?
Ok, teraz pokaże Ci na prostym przykładzie jak sprawdzić homogeniczność wariancji.
- Uruchom jamovi i wklej swoje dane
- Plik → Nowy.
- Kliknij w komórkę A1 i wciśnij Ctrl+V (wklej swój blok z dwiema kolumnami: u mnie to : kierunek, czas_zadania_s).
- Jeśli masz cztery kolumny pracuj na jednej parze naraz:
- lewa para = kierunek_A + czas_A,
- prawa para = kierunek_B + czas_B.
Zbędne/puste kolumny usuń (prawy klik w nagłówek → Usuń).
- Ustaw poprawne typy zmiennych
- Kliknij ikonkę przy nazwie kolumny:
- kierunek → Nominalny (kategorie/tekst),
- czas_zadania_s → Ciągły (liczba).
- To ważne, bo wykresy i statystyki włączają się dopiero przy prawidłowych typach.
- Kliknij ikonkę przy nazwie kolumny:
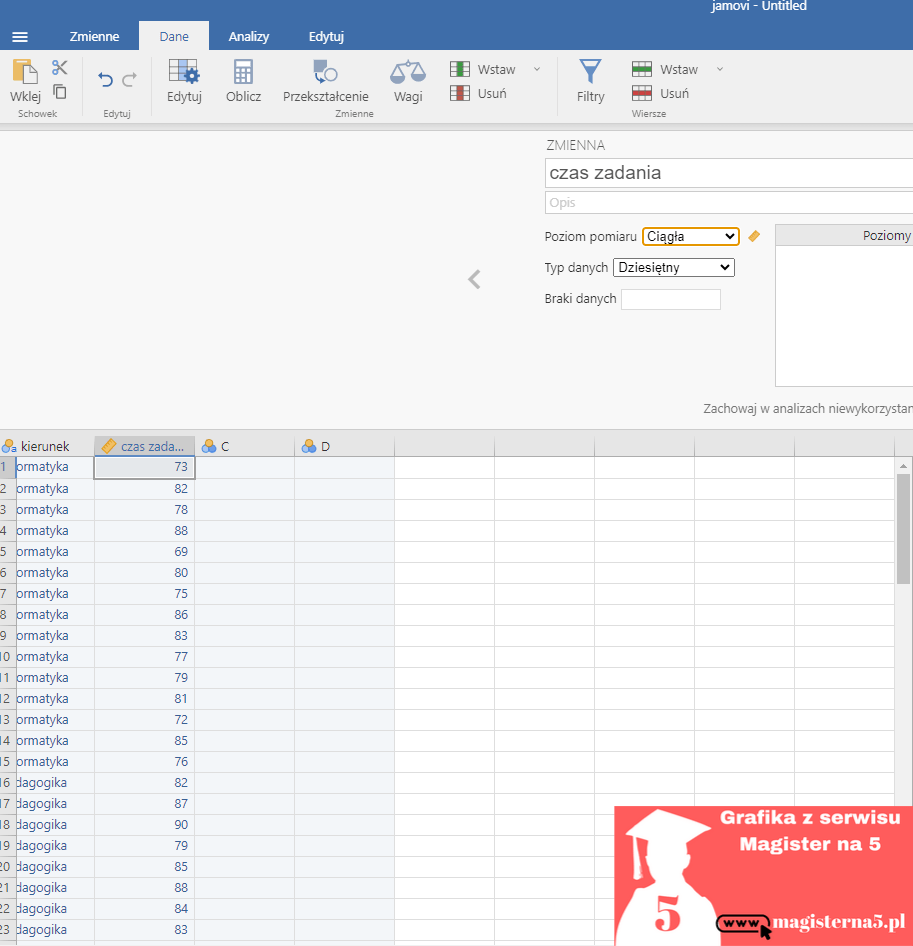
W tym momencie powinno to wyglądać tak:
Wejdź do statystyk opisowych (Opisowe)
- Analizy → (Eksploracja) → Opisowe (czasem jest po prostu „Opisowe” bez „Eksploracji”).
- Upewnij się, że w polu „Statystyki opisowe” masz „Zmienne w kolumnach” (to domyślne).
Wybierz zmienne do analizy
- Przeciągnij czas_zadania_s (albo czas_A/czas_B) do pola Zmienne.
- Przeciągnij kierunek (albo kierunek_A/kierunek_B) do Podziel według (Split by).
Włącz boxplot (wykres pudełkowy)
- Rozwiń sekcję Wykresy (mały trójkąt).
- Zaznacz Wykres skrzynkowy.
- (Polecam) zaznacz Oznacz przypadki odstające i Dane – zobaczysz punkty i outliery.
Spójrz na przykład:
Włącz odchylenie standardowe (SD)
- Rozwiń sekcję Statystyki.
- Zaznacz Odchylenie standardowe.
- W tabelce po prawej zobaczysz SD dla każdej grupy. Wiersz „kierunek = NaN” to nagłówek – ignoruj; liczą się wartości przy nazwach grup (np. Informatyka, Pedagogika, Zarządzanie).
Tak to wygląda na przykładzie:
Szybka interpretacja homogeniczności wariancji
- Boxplot: podobna wysokość pudełek i wąsów = podobny rozrzut; jedno znacząco wyższe/szersze = większy rozrzut w tej grupie.
- SD: jeśli największe SD nie przekracza ok. 2× najmniejszego, zwykle jest OK dla klasycznych testów; gdy przekracza → podejrzenie nierówności wariancji.
W przypadku moich danych, przedstawionych na rysunkach powyżej (Inf ≈ 5.42, Ped ≈ 3.74, Zarz ≈ 16.5)? Różnice są duże → „na oko” wariancje nierówne.
Boxplot. Na wykresie pudełkowym widać, że Informatyka i Pedagogika mają bardzo zbliżony rozrzut wyników – pudełka są niskie, „wąsy” krótkie. Z kolei Zarządzanie ma wyraźnie wyższe pudełko i dłuższe wąsy (zakres od ~60 do ~120 s), co oznacza dużo większą zmienność w tej grupie. To już „na oko” sugeruje, że rozrzuty nie są równe między grupami.
Odchylenia standardowe (SD).
- Informatyka: SD ≈ 5,42
- Pedagogika: SD ≈ 3,74
- Zarządzanie: SD ≈ 16,5
Stosunek największego SD do najmniejszego to 16,5 / 3,74 ≈ 4,4. To znacznie więcej niż 2, więc różnice w rozrzutach są istotne praktycznie (Zarządzanie „rozsypane” najmocniej).
Wniosek. Dane nie spełniają założenia homogeniczności wariancji (równości rozrzutów między grupami). W dalszej analizie porównania średnich, zamiast klasycznej ANOVA należy użyć ANOVA Welcha (albo – przy dwóch grupach – test t Welcha). Dodatkowo warto potwierdzić wniosek testem Levene’a; jeśli wyjdzie p < 0,05, formalnie mamy nierówne wariancje.
Gotowe zdanie do pracy (wstaw wyniki testu):
„Ocena rozrzutu (boxplot, SD: Inf. ≈ 5,42; Ped. ≈ 3,74; Zarz. ≈ 16,5) wskazała nierówność wariancji między grupami. Test Levene’a potwierdził różnice (F(…)=…, p < 0,05), dlatego zastosowano ANOVA Welcha.”
Proste, prawda?
Opcjonalnie Test formalny: Levene (test homogeniczności)
- Analizy → ANOVA → Jednoczynnikowa ANOVA.
- czas_zadania → Zmienne zależne, kierunek → Zmienna grupująca.
- Wariancje: zaznacz Nie zakładaj równości (test Welcha).
- Weryfikacja założeń: zaznacz Test homogeniczności (to Levene).
- (Opcjonalnie) w „Statystyki” zaznacz Różnica średnich i Wyświetl istotność statystyczną.
Spójrz na przykład:
Z obliczeń wynika:
- Test homogeniczności wariancji Levene’a:
F(2, 42) = 12.3, p < .001
→ Wariancje nie są równe. Decyzja: należy użyć ANOVA Welcha (odporna na nierówne wariancje).
ANOVA Welcha (porównanie średnich wielu grup)
- Jednoczynnikowa ANOVA (test Welcha):
F(2, 24.5) = 7.67, p = .003
→ Co najmniej jedna średnia czasu różni się od pozostałych (istotnie statystycznie).
Co dalej?
Należy Uruchomić post-hoc Gamesa-Howella, by sprawdzić które pary (np. Zarządzanie vs Informatyka, Zarządzanie vs Pedagogika, Informatyka vs Pedagogika) różnią się średnią i odczytać p-value dla każdej pary.
Jak homogeniczność wariancji opisać w pracy magisterskiej?
- Dla pliku „równe”:
„Przed analizą sprawdzono homogeniczność wariancji testem Levene’a (p ≥ 0,05), co uprawnia do zastosowania klasycznej analizy wariancji.” - Dla pliku „nierówne”:
„Test Levene’a wskazał nierówność wariancji (p < 0,05); zastosowano ANOVA Welcha, która nie wymaga założenia równości wariancji.”
Gdy wariancje są nierówne. To nie koniec świata. Zamiast klasycznego t-testu/ANOVA używasz wersji Welcha (t-test Welcha dla 2 grup, ANOVA Welcha dla 3+). Alternatywnie czasem pomaga prosta transformacja zmiennej (np. logarytm przy „lejkowatych” resztach), a gdy skale są mocno „nienormalne” – testy nieparametryczne.
Ważne: w pracy napisz jedno zdanie, że sprawdziłaś/eś równość wariancji i na tej podstawie wybrałaś/eś właściwy test. To cała magia.
Gdy wariancje są nierówne – co dalej?
Jeśli w teście Levene’a wyszło p < 0,05, to znaczy, że grupy „rozsypują się” różnie. Klasyczne porównania średnich mogą wtedy kręcić nosem. Rozwiązanie? Zmień tryb na wersje odporne — to dosłownie dwa kliknięcia, zero dramatu.
Dwie grupy → t-test Welcha.
To jest zwykły t-test, tylko nie udaje, że wariancje są równe.
W jamovi: Testy t → Niezależne → dodaj zmienne → w „Założeniach” zostaw Levene, a w wynikach czytaj wiersz Welcha (albo zaznacz opcję „Welch”). Do pracy wpisujesz: „Zastosowano t-test Welcha z powodu nierówności wariancji”.
Trzy lub więcej grup → ANOVA Welcha.
W jamovi: ANOVA → Jednoczynnikowa → zaznacz Nie zakładaj równości (test Welcha).
Chcesz wiedzieć które pary się różnią? W „Testy post-hoc” wybierz Gamesa–Howella (on też nie wymaga równych wariancji). W pracy: „Użyto ANOVA Welcha; porównania par wykonano testem Gamesa–Howella.”
A jeśli dane są mocno skośne albo to skala porządkowa?
Masz dwa proste wyjścia:
- Transformacja (np. log czasu lub kwot) i dopiero test; pamiętaj, że wtedy opisujesz wynik „po logu” albo pokazujesz też mediany.
- Testy nieparametryczne: dla 2 grup Mann–Whitney, dla 3+ Kruskal–Wallis; raportuj medianę + IQR (rozstęp międzykwartylowy).
Jedno zdanie do wklejenia:
„Ponieważ test Levene’a wykazał nierówność wariancji (p < 0,05), zastosowano odpowiednio t-test/ANOVA Welcha; w analizach par użyto Gamesa–Howella. Wyniki potwierdziły/nie potwierdziły istotnych różnic między grupami (…podać wartości).”
Jak homogeniczność wariancji opisać w pracy magisterskiej?
Mini-case’y homogeniczności wariancji (4 szybkie przykłady z liczbami)
🏥 Zdrowie — czas oczekiwania w 3 oddziałach
- Dane: A=35±7 min, B=41±8 min, C=58±20 min.
- Levene: p < 0,001 → wariancje nierówne.
- Analiza: ANOVA Welcha → F=9,2; p=0,001. Gamesa-Howella: C>A (p<0,01), C>B (p<0,01).
- Jedno zdanie: „Z powodu nierówności wariancji użyto Welcha; oddział C miał istotnie dłuższy czas oczekiwania.”
👔 HR — poziom stresu (1–5) w 3 działach
- Dane: Dział1=3,1±0,5; Dział2=3,2±0,6; Dział3=3,9±1,1.
- Levene: p=0,02 → nierówne.
- Analiza: Welch ANOVA → F=5,4; p=0,008. Gamesa-Howella: D3 > D1 (p=0,01), D3 > D2 (p=0,03).
- Jedno zdanie: „Najwyższy stres w Dziale 3; zastosowano Welcha.”
💻 IT/UX — czas zadania w 3 prototypach
- Dane: P1=52±10 s, P2=49±9 s, P3=61±22 s.
- Levene: p=0,01 → nierówne.
- Analiza: Welch ANOVA → F=4,7; p=0,013. Gamesa-Howella: P3 > P2 (p=0,02).
- Jedno zdanie: „Prototyp 3 był istotnie wolniejszy.”
🎓 Edukacja — wynik testu (2 metody nauczania)
- Dane: Metoda A=72±9 pkt, Metoda B=78±10 pkt.
- Levene: p=0,38 → równe.
- Analiza: t-test klasyczny → t=2,1; p=0,04.
- Jedno zdanie: „Metoda B dała wyższy wynik; równość wariancji spełniona.”
Jeśli masz już boxploty, odchylenia standardowe i wynik Levene’a, to… temat masz ogarnięty. Homogeniczność wariancji to tylko pytanie: czy grupy „rozsypują się” podobnie. Gdy tak – jedziesz klasycznym t-testem/ANOVA. Gdy nie – Welch ratuje sytuację (a przy parach Gamesa-Howella). I już.
Homogeniczność wariancji w pracy magisterskiej podsumowanie
I to tyle — krótko, konkretnie i po studencku. Teraz Twoja kolej: otwórz swój arkusz, wrzuć prawdziwe dane (czas dojazdu, godziny snu, wydatki z tygodnia) i sprawdź, co pokaże środek. Zobaczysz, że mediana często mówi więcej niż „ładna” średnia.
Na obronie możesz powiedzieć: „Najpierw sprawdziłam/em równość wariancji, potem dobrałam/em właściwy test.” Brzmi poważnie, a to po prostu dobry nawyk. Powodzenia – i niech Twoje dane rozrzucają się… w kontrolowany sposób. 😄📊
Trochę już wiem o homogeniczności wariancji w pracy magisterskiej. Teraz chcę poznać proces pisania
Naucz się pisać pracę w godzinę. Sprawdź e-book.
Jak napisać pracę w tydzień?
E-book- Jak napisać pracę dyplomową w tydzień? Pobieram teraz>>
Pobieram teraz>>
Dlaczego ten e-book może Ci bardzo pomóc?
- 85 stron samych konkretów- materiał do błyskawicznego wykorzystania.
- Pokaże Ci jak zacząć już za 5 minut. Bez zastanawiania się i marnowania czasu.
- Pokonasz perfekcjonizm i przestaniesz okładać na później.
- Dowiesz się jak pisać pracę 10 razy szybciej, stosując metodę Magistra na 5.
- Uprościliśmy temat, jak tylko się dało. Zrozumiesz, nawet jak nigdy nie pisałeś żadnej pracy.
- Przeczytasz w godzinę. Już nie musisz marnować czasu na dojazdy na uczelnie i seminaria.
- Dostęp w 30 sekund. Materiał dostaniesz w prosto na maila.
- Dostajesz dostęp do wszystkich aktualizacji. Ten produkt to mój absolutny priorytet. Cały czas go ulepszam i dodaje nowe materiały.
- Dużo przykładów. Nie wymyślasz nic od nowa.
- Schematy i wzory działania. Prowadzimy Cię jak po sznurku.
- Dodatkowe ćwiczenia. Zaczniesz działać już na 5 minut.
- Za cenę 4 kaw w Żabce.
Potrzebujesz pomocy z najtrudniejszą częścią swojej pracy?
Metodologia, rozdział badawczy, analiza statystyczna. Błyskawiczna pomoc>>
--
Zobacz opinie:
Zobacz, jakie materiały mogę Ci jeszcze zaproponować.
–>Sklep Magistra na 5
Jeżeli potrzebujesz pomocy, po prostu napisz.
–> Wyślij pytanie








 Pobieram teraz>>
Pobieram teraz>>




