Ostatnia aktualizacja 10 października 2025
Masz średnią z ankiety i myślisz: „Brzmi nieźle… ale na ile mogę temu zaufać?” Tu wchodzi błąd standardowy (SE) – prosta liczba, która mówi, jak precyzyjna jest Twoja średnia. Dzięki SE odróżnisz wynik „z przypadkowym drżeniem” od takiego, który naprawdę trafia w sedno.
W kilka minut zobaczysz, jak SE pomaga budować przedziały ufności, robić pewniejsze wnioski i pisać „Wyniki”, które promotor czyta z uśmiechem. Zaczynamy bez żargonu – krótko, jasno i po studencku.
Potrzebujesz szybkiej pomocy z obliczeniem błędu standardowego w pracy magisterskiej? Kliknij poniżej
–> Błąd standardowy w pracy magisterskiej. Błyskawiczna pomoc
–> Wzory rozdziałów badawczych ze statystyką
Nie wiem, jak zacząć. Masz coś dla mnie?
–> E-book- Jak Napisać Pracę Dyplomową W Tydzień
–> Pobierz przykładową pracę licencjacką
Prosta definicja błędu standardowego w statystyce
Błąd standardowy (SE) to miara jak bardzo może „chybiać” Twoja średnia z próby.
Wyobraź sobie, że robisz tę samą ankietę 100 razy na nowych, losowych grupach tej samej wielkości — każda średnia wyjdzie ciut inna. SE to typowy rozmiar tych wahań. Im mniejszy SE, tym precyzyjniejsza Twoja średnia.
- SE maleje, gdy rośnie liczba badanych (N) — więcej osób = pewniejszy wynik.
- SE to nie SD: SD opisuje rozrzut odpowiedzi osób, a SE — niepewność średniej.
- Intuicyjnie (dla średniej): SE ≈ SD / √N.
Przykład: SD=12, N=100 → SE ≈ 12/10 = 1,2 (średnia „drży” o ~1,2 punktu).
SE vs SD -nie myl!
SD = rozrzut ludzi.
Wyobraź sobie grupę studentów i ich wyniki ze stresu. Jedni mają 20, inni 80. Odchylenie standardowe (SD) mówi, jak rozstrzelone są te pojedyncze wyniki. Duże SD = ludzie bardzo się różnią; małe SD = są do siebie podobni.
SE = niepewność średniej.
Teraz liczysz jedną liczbę: średni stres całej grupy. Gdybyś losował/a drugą taką samą grupę i znowu liczył/a średnią, wyszłaby trochę inna. Błąd standardowy (SE) mówi, jak bardzo ta średnia „drży” między takimi powtórkami. To precyzja Twojej średniej.
Kluczowa różnica:
- SD opisuje rozrzut osób.
- SE opisuje pewność średniej.
Dlaczego SE maleje, gdy rośnie N?
Im więcej osób w próbie, tym średnia jest stabilniejsza (pojedyncze „odloty” mniej ją ruszają). Dlatego SE spada przy większym N — masz większą pewność swojego wyniku.
Mini-przykład:
- 10 osób, SD = 12 → średnia może „skakać” wyraźnie (SE spore).
- 100 osób, to samo SD = 12 → średnia „skacze” dużo mniej (SE małe).
Zapamiętaj: SD = „jak różni są ludzie”, SE = „jak pewna jest średnia”. Więcej osób = mniejszy SE = pewniejszy wniosek.
Dlaczego błąd standardowy jest ważne w pracy dyplomowej?
Bo mówi na ile możesz ufać swojej średniej. Sama średnia to „strzał w punkt”, a SE (błąd standardowy) dodaje info o precyzji tego strzału.
Gdzie użyć błędu standardowego w pracy magisterskiej?
- Opis próby: średnia + SE + 95% PU (np. poziom stresu, wiek).
- Główne wyniki: obok testów i p-value pokaż SE/PU, żeby widać było precyzję.
- Wykresy: słupki ± SE lub ± PU.
Jak to wpisać (gotowiec)
„Średni poziom stresu wyniósł M = 59,6, SE = 1,2, 95% PU: 57,2–62,0 (N = 120).
Węższy przedział sugeruje wysoką precyzję oszacowania.”
Jak w jamovi policzyć SE (błąd standardowy) – krok po kroku
- Otwórz dane w jamovi (moja kolumna ze zmienną liczbową nazywa się np. stres).
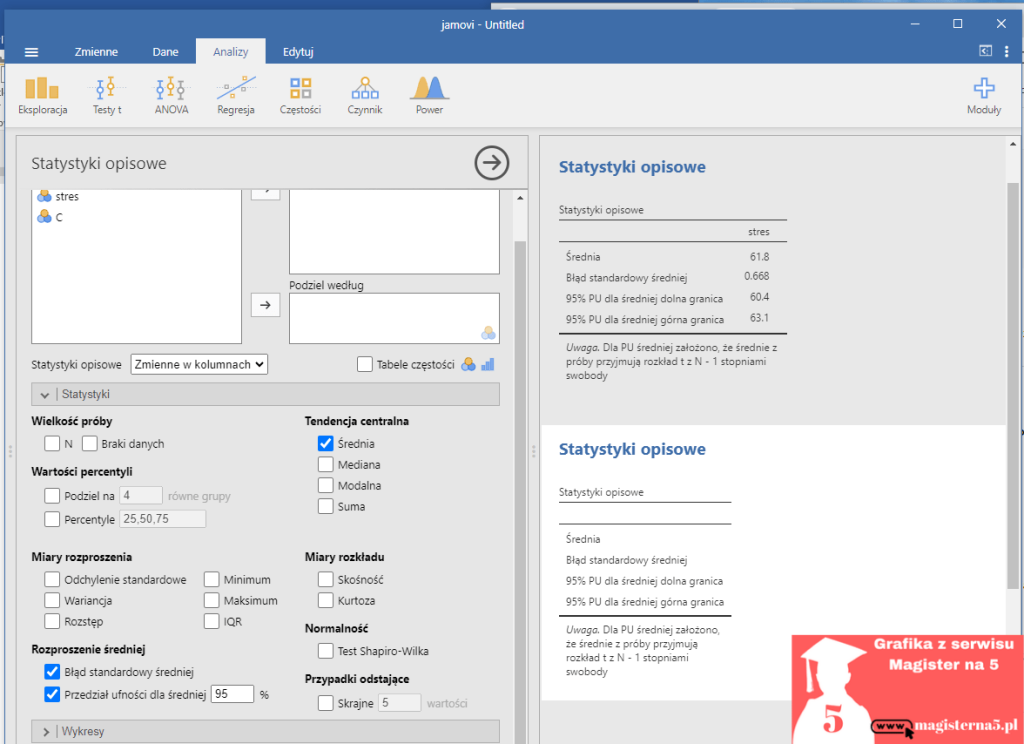
Jeśli wszystko jest ok, przy nazwie stres powinna być ikonka 123 (czyli typ liczbowy). - Na górze kliknij Analizy, a potem Eksploracja → Statystyki opisowe.
Po lewej zobaczysz listę zmiennych, po prawej puste pole analizy. - Przeciągnij stres z listy po lewej do pola Zmienne po prawej.
W tym momencie jamovi wie, co ma policzyć. - W sekcji z opcjami (po lewej, niżej) zaznacz:
- Średnia (żeby pokazać wartość M),
- Błąd standardowy średniej (to jest właśnie SE),
- Przedział ufności dla średniej 95%,
- N (wielkość próby), żeby w tabeli było widać, ile osób weszło do obliczeń.
- Spójrz na mój przykład i na tabelę wyników po prawej.
U mnie wyszło:
Średnia = 61,8, Błąd standardowy średniej (SE) = 0,668, 95% PU: 60,4–63,1.
Chcesz SE dla każdej grupy (np. Dzienni vs Zaoczni)? W tym samym oknie przeciągnij zmienną grupującą (np. tryb) do pola Podziel według. Dostaniesz osobne tabelki M, SE i 95% PU dla każdej grupy.
Co z tego wynika (czytanie wyniku SE)
- SE = 0,668 mówi, jak bardzo może „drżeć” Twoja średnia między różnymi losowaniami próby o tej samej wielkości. Czyli średnia 61,8 jest dość precyzyjna – waha się typowo o ok. 0,67 punktu.
- Z SE wynika 95% przedział ufności: 60,4–63,1. To jest elegancki sposób, by powiedzieć: „prawdziwa średnia w populacji jest najpewniej gdzieś w tym zakresie”.
- Im mniejszy SE, tym węższy przedział ufności i pewniejszy wynik. Najprostsza droga do mniejszego SE to większe N (więcej badanych) lub mniejszy rozrzut odpowiedzi (lepsze, stabilniejsze pomiary).
Jak to zapisać w pracy ?
Wersja podstawowa (cała próba):
„Średni poziom stresu wyniósł M = 61,8, SE = 0,67, 95-procentowy przedział ufności: 60,4–63,1 (N = …). Wynik wskazuje na dobrą precyzję oszacowania średniej (wąski przedział ufności).”
Wersja z grupami (jeśli używasz „Podziel według”):
„Dzienni: M = …, SE = …, 95% PU: …–…, N = …; Zaoczni: M = …, SE = …, 95% PU: …–…, N = …. Różnice interpretowano z uwzględnieniem szerokości przedziałów ufności (precyzji oszacowań).”
Małe przypomnienie, żeby nie pomylić
- SD (odchylenie standardowe) = rozrzut osób;
- SE (błąd standardowy) = niepewność średniej.
Do raportu wrzucaj M + SE + 95% PU + N – promotor będzie zadowolony, a Ty masz czysty, rzetelny opis.
Najczęstsze pomyłki przy liczeniu błędu standardowego
Błąd standardowy pracy magisterskiej podsumowanie
Błąd standardowy to Twoja linijka do mierzenia precyzji. Sama średnia mówi „ile”, a SE dopowiada „na ile pewnie”. Jeśli w „Wynikach” pokażesz M + SE + 95% PU + N, od razu widać, że wiesz, co robisz — to jest rzetelne i „promotor-proof”.
W praktyce: w jamovi włącz „Błąd standardowy” i „Przedział ufności”, odczytaj liczby i zapisz je jednym, prostym zdaniem. Pamiętaj, tylko by nie mylić SE z SD i zawsze podawać N. Tyle. Zero magii, same konkrety — a Twoje statystyki zyskają klasę.