Założenia testów statystycznych w pracy magisterskiej. Co musisz sprawdzić, zanim klikniesz „Analizuj”

Ostatnia aktualizacja 10 października 2025

Wyobraź sobie, że jedziesz autem bez prawa jazdy. Niby jedzie… ale do pierwszej kontroli. Tak samo jest ze statystyką: test „jedzie”, jeśli spełnione są założenia. Gdy je olejesz, możesz „zobaczyć” efekt, którego nie ma (fałszywy alarm) albo przegapić prawdziwy (auć).

Dobra wiadomość? To nie fizyka kwantowa. Kilka prostych checków i wiesz, czy można ufać p-value. W tym tekście pokażę Ci, co sprawdzić, jak sprawdzić i co zrobić, jeśli nie gra. Krótkie zdania, zero żargonu, trochę humoru. Czytaj dalej i zrób swojej statystyce przegląd techniczny, zanim wciśniesz „Analizuj”. 🚗📊

Potrzebujesz szybkiej pomocy z obliczeniem testów statystycznych w swojej pracy dyplomowej? Kliknij poniżej
–> Testy statystyczne do pracy magisterskiej. Błyskawiczna pomoc
–> Wzory rozdziałów badawczych ze statystyką

Nie wiem, jak zacząć. Masz coś dla mnie?
–> E-book- Jak Napisać Pracę Dyplomową W Tydzień
–> Pobierz przykładową pracę licencjacką

Definicja założeń testów statystycznych (po ludzku)

Założenia testu statystycznego to zestaw warunków, które powinny być w miarę spełnione, żeby wynik testu (p-value, wnioski) był wiarygodny.
To takie „reguły gry” dla danych: jeśli grasz zgodnie z nimi, możesz ufać wynikom; jeśli nie — ryzykujesz fałszywy alarm albo przegapienie prawdziwego efektu.

Po co badać założenia testów statystycznych w pracy dyplomowej?

Bo chcesz mieć wyniki, którym można ufać, a nie „statystykę na chybił-trafił”.

• Uczciwe wnioski: sprawdzasz założenia i wiesz, kiedy p-value ma sens, a kiedy robi z Ciebie żarty.
• Profesjonalny opis: w Metodologii i Wynikach pokażesz, że to była analiza, nie „wróżenie z Excela”.
• Obrona bez stresu: na pytanie promotora „Sprawdziła/łeś założenia?” odpowiadasz spokojnie: „Tak — i mam to w tekście”.

Zdanie do wklejenia (Metodologia)

„Przed testami sprawdziłam/sprawdziłem założenia: normalność (Shapiro–Wilka), równość wariancji (Levene’a) i niezależność obserwacji. Gdy coś nie grało, używałam/używałem wersji odpornych (Welch, Mann–Whitney, Kruskal–Wallis) i raportowałam/raportowałem siłę efektu z 95% przedziałami ufności.”

Kiedy nie ma sensu się spinać?

Są sytuacje, w których nie trzeba robić doktoratu z założeń — wystarczy zdrowy rozsądek:

• Masz bardzo dużą próbę.
  Delikatna nienormalność danych zwykle nie zabije testu (działa „magia” CLT). Sprawdź wykresy, idź dalej.
• Od razu używasz wersji odpornej.
  Nierówne wariancje? t-Welcha. Skale porządkowe lub brak normalności? Mann–Whitney (2 grupy) albo Kruskal–Wallis (3+). Nieliniowość? Spearman zamiast Pearsona. I po sprawie.
• Zawsze zostaw ślad w pracy.
  Napisz krótko, co sprawdziłaś/eś i dlaczego wybrałaś/eś plan B. To pokazuje, że wiesz, co robisz — i promotor nie ma o co się czepiać.

Dla jakich kierunków założenia testów statystycznych (i po co)?

Psychologia i pedagogika

Tu bardzo często porównasz dwie lub trzy grupy (t-test, ANOVA) albo sprawdzasz, czy dwie rzeczy idą ze sobą w parze (korelacja). Dlatego warto rzucić okiem, czy rozkłady w grupach są w miarę „dzwonowe” i czy rozrzuty nie różnią się dramatycznie. Jeśli wszystko gra, klasyczne testy robią robotę. Jeśli nie — nie ma dramatu: bierzesz wersję odporną (np. t-Welcha) albo nieparametryczną (Mann–Whitney, Kruskal–Wallis) i jedziesz dalej. W opisie napisz po prostu, że sprawdziłaś/eś założenia i świadomie wybrałaś/eś plan B.

Medycyna i pielęgniarstwo

Tu często liczysz odsetki (np. ilu pacjentów poprawiło wynik) i pracujesz na tabelach 2×2. To oznacza, że interesują Cię „liczności oczekiwane” w komórkach — jeśli są małe, test χ² może przesadzić z pewnością. Wtedy wjeżdża test Fishera i sprawa załatwiona. Przy regresji (np. przewidywanie ryzyka) rzuć okiem na reszty: czy mają podobny rozrzut w całym zakresie (homoscedastyczność). Jeden akapit o tym w Metodologii i promotor odhacza: „jest solidnie”.

Ekonomia, zarządzanie, marketing

Dużo ANOVA, regresji i testów A/B. Dane bywają kapryśne: jedna firma „odstaje”, jedna kampania „wystrzeliła” i psuje linię. Dlatego sprawdzasz liniowość, wariancje i obserwacje odstające (czy nie ciągną wyniku). Gdy jest krzywo — użyj wersji Welcha, Spearmana albo regresji z odpornymi błędami. Dzięki temu Twoje wnioski są nie tylko „istotne statystycznie”, ale też wiarygodne biznesowo.

Nauki techniczne, IT

Często mierzysz czasy, kliki, błędy — dane bywają skośne i pełne „dziwnych” rekordów. Zanim odpalisz klasyczny t-test, sprawdź, czy to w ogóle sensowne (może skala porządkowa? może rozkład mocno skośny?). Jeśli tak, super. Jeśli nie, prosty manewr: testy porządkowe (Mann–Whitney), transformacja (np. log) albo miary odporne. Dwie minuty takiej kontroli i Twoje A/B ma nogi.

Nauki społeczne i humanistyczne

Często masz małe próby, skale Likerta i „prawie liczby”. To idealne środowisko dla testów odpornych. Możesz od razu planować Manna–Whitneya zamiast t-testu, Kruskala–Wallisa zamiast ANOVA i Spearmana zamiast Pearsona. Nie dlatego, że „tak trzeba”, tylko dlatego, że te narzędzia lepiej znoszą realne dane. Wystarczy krótko napisać, co sprawdziłaś/eś i dlaczego wybrałaś/eś właśnie te testy.

Obliczenie założeń testów statystycznych w Jamovi

Co zakłada (po ludzku):
W każdej grupie rozkład wyników jest „w miarę dzwonowy” (normalność, zwłaszcza przy małym N) i rozrzut w obu grupach jest podobny (równość wariancji).

Jak sprawdzić w jamovi:
Analizy → Testy t → Niezależne próbki t

• Zaznacz „Test normalności (Shapiro–Wilka)” i „Test homogeniczności (Levene’a)”.
• Dodatkowo włącz „Statystyki opisowe” i rzuć okiem na histogram/QQ-plot (Analizy → Eksploracja).

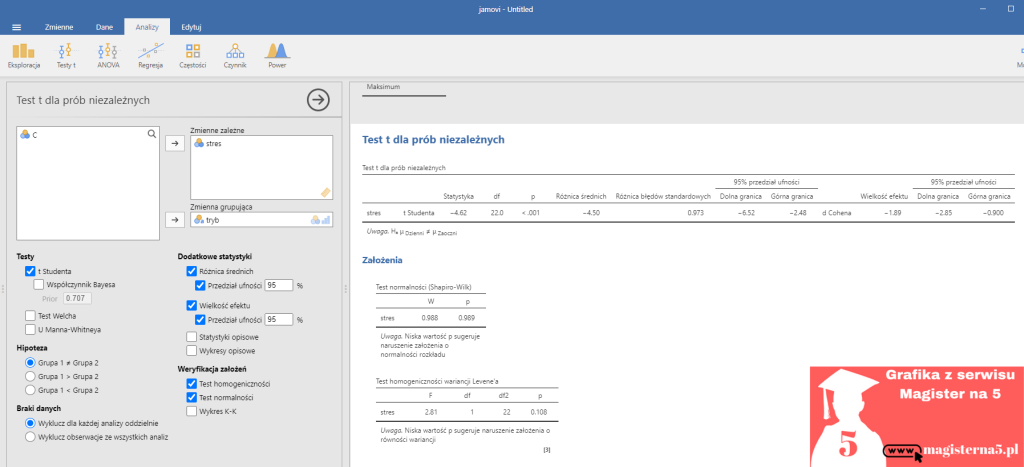
Co tu jest najważniejsze?

• Test: t dla prób niezależnych (dwustronny).
• Wynik: t(22) = −4,62, p < .001 → są mocne dowody na różnicę między grupami.
• Różnica średnich: −4,50 z 95% PU: −6,52 do −2,48.
• Siła efektu (d Cohena): −1,89 z 95% PU: −2,85 do −0,90 → efekt bardzo duży (prawie 2 odchylenia standardowe).
• Założenia:
  • Normalność (Shapiro–Wilka): p = 0,989 → OK.
  • Równość wariancji (Levene’a): p = 0,108 → OK.
    → Możesz raportować klasyczny t-Studenta.

Uwaga o znaku (−)

W jamovi „Różnica średnich” to Grupa 1 − Grupa 2. Masz −4,50, więc Grupa 1 ma średnio ~4,5 punktu mniej niż Grupa 2.
Najczęściej Grupa 1 = pierwszy poziom zmiennej tryb (np. Dzienni), a Grupa 2 = Zaoczni. Jeśli chcesz mieć 100% pewności, zerknij chwilę w Analizy → Eksploracja → Statystyki opisowe i odczytaj średnie każdej grupy.

Jak to zapisać w pracy ?

Wersja z nazwami grup (gdy Grupa 1 = Dzienni, Grupa 2 = Zaoczni):

„Porównano poziom stresu u studentów dziennych i zaocznych testem t dla prób niezależnych. Wynik był istotny, t(22) = −4,62, p < .001.
Średnia różniła się o −4,50 punktu (95% PU: −6,52; −2,48), co odpowiada bardzo dużej sile efektu, d = −1,89 (95% PU: −2,85; −0,90).
Założenia testu były spełnione: Shapiro–Wilka p = 0,989, Levene’a p = 0,108.”

Wersja neutralna (gdy nie chcesz wskazywać kierunku grup):

„Test t dla prób niezależnych wykazał istotną różnicę między grupami, t(22) = −4,62, p < .001; różnica średnich = −4,50 (95% PU: −6,52; −2,48), d = −1,89 (95% PU: −2,85; −0,90). Założenia testu spełnione.”

Co dalej (jeśli chcesz domknąć temat)

• Dodaj tabelę/wykres z średnimi i 95% PU dla każdej grupy (ładnie wygląda i jest czytelne).
• W Dyskusji napisz jednym zdaniem, co to znaczy praktycznie (np. „tryb studiów może wiązać się z obciążeniem i organizacją dnia, co przekłada się na stres”).

Gdyby kiedykolwiek Levene p < .05, przełącz „Test Welcha” i raportuj wersję Welcha (zastępuje klasyczny t). Tu nie musisz — założenia są OK.

t-test (założenia spełnione)

„Rozkłady nie odbiegały od normalności (test Shapiro–Wilka: p > 0,05), a równość wariancji potwierdzono (test Levene’a: p = 0,41). Zastosowano test t dla prób niezależnych: t(df) = …, p = …, d = … (95% PU: …–…).”

t-test Welcha (wariancje różne)

„Założenie równości wariancji nie zostało spełnione (test Levene’a: p = 0,01), dlatego zastosowano test t Welcha: t(dfWelcha) = …, p = …, d = … (95% PU: …–…).”

Test nieparametryczny (dane nienormalne / skala porządkowa)

„Ze względu na odchylenie od normalności rozkładu zastosowano test Manna–Whitneya: U = …, p = …. Raportowano siłę efektu r = … (95% PU: …–…).”

ANOVA klasyczna (założenia spełnione)

„Równość wariancji została spełniona (Levene: p > 0,05). Wykonano jednoczynnikową ANOVA: F(df1, df2) = …, p = …, ηp² = …; w przypadku istotności zastosowano testy post-hoc … .”

ANOVA Welcha / Kruskal–Wallis (plan B)

„Ze względu na brak równości wariancji przeprowadzono ANOVA Welcha: FWelcha(df1, df2) = …, p = …, ηp²/ω² = ….”
albo
„Ze względu na nienormalność rozkładów zastosowano test Kruskala–Wallisa: H(df) = …, p = …. Raportowano rangi średnie i porównania post-hoc.”

Korelacja / regresja liniowa (założenia spełnione)

„Zweryfikowano liniowość oraz jednorodność rozrzutu reszt na wykresach diagnostycznych; założenia były spełnione. Korelacja Pearsona: r = …, p = …, 95% PU: …–…. (lub) Regresja liniowa: B = …, SE = …, t(df) = …, p = …; R² = … .”

Regresja z błędami odpornymi (heteroscedastyczność)

„Stwierdzono heteroscedastyczność reszt; wyniki raportowano z odpornymi błędami standardowymi (HC): B = …, SE(HC) = …, t(df) = …, p = …; R² = … .”

Założenia testów statystycznych podsumowanie

Założenia testów to nie „papierologia”, tylko pasy bezpieczeństwa Twojej analizy. Sprawdzasz je po to, by mieć pewność, że p-value i wnioski naprawdę coś znaczą. Gdy wszystko gra — jedziesz klasycznym testem. Gdy zgrzyta — wybierasz wersję odporną i jedziesz dalej, ale świadomie.

Weź to na skróty: rzut oka na normalność (Shapiro + wykres), równość wariancji (Levene), liniowość i reszty w regresji, sensowne liczności dla χ². Jeśli coś nie pasuje, przełącz na Welcha, Manna–Whitneya, Kruskala–Wallisa, Spearmana albo użyj błędów odpornych. I koniecznie zapisz to w Metodologii jednym spokojnym zdaniem.

Na końcu zawsze raportuj pakiet „promotor-proof”: test + p + siła efektu + 95% przedział ufności + krótka informacja o założeniach/planie B. Zero magii, czysta higiena statystyczna. Dzięki temu Twoje wyniki są czytelne, rzetelne i gotowe do obrony — a Ty możesz spokojnie dopić kawę. ☕📊

Trochę już wiem o liczeniu założeń testów statystycznych. Teraz chcę poznać proces pisania

Naucz się pisać pracę w godzinę. Sprawdź e-book.

Zobacz, jakie materiały mogę Ci jeszcze zaproponować.
–>Sklep Magistra na 5

Jeżeli potrzebujesz pomocy, po prostu napisz.
–> Wyślij pytanie

Nie zapomnij o prezencie!