Ostatnia aktualizacja 17 września 2025
Średnia arytmetyczna w pracy magisterskiej. O co chodzi?
Wyobraź sobie, że masz całą górę danych z ankiety, testów, badań czy ocen… i kompletnie nie wiesz, jak z tego zrobić coś sensownego. Tu wjeżdża średnia arytmetyczna – jak kumpel, który zawsze pomoże Ci ogarnąć chaos. Dzięki niej w sekundę wiesz, “jaki jest przeciętny wynik”, możesz porównywać grupy i napisać coś mądrze brzmiącego w rozdziale z wynikami, zamiast tonąć w liczbach.
Średnia to taki fast food w statystyce – szybka, prosta, każdy ją rozumie i zawsze znajdzie się dla niej miejsce w Twojej pracy. Co najlepsze, policzysz ją w Excelu na dwa kliknięcia, a promotor będzie zadowolony, że potrafisz wyciągnąć z danych coś więcej niż tylko surowe tabelki.
W tym artykule pokażę Ci, czym naprawdę jest średnia, jak ją liczyć (wzór i Excel krok po kroku), gdzie ją wykorzystać w pracy dyplomowej i jak o niej pisać, żeby brzmiało to profesjonalnie, ale bez zbędnego nadęcia. 🚀
Potrzebujesz szybkiej pomocy z obliczeniem mediany w swojej pracy dyplomowej? Kliknij poniżej
–> Średnia arytmetyczna do pracy magisterskiej. Błyskawiczna pomoc
–> Wzory rozdziałów badawczych ze statystyką
Nie wiem, jak zacząć. Masz coś dla mnie?
–> E-book- Jak Napisać Pracę Dyplomową W Tydzień
–> Pobierz przykładową pracę licencjacką
Co to jest średnia arytmetyczna?
Średnia arytmetyczna to nic innego jak:
“przeciętna” wartość liczb, które mamy pod ręką. Bierzesz wszystkie swoje wyniki, dodajesz je do siebie i dzielisz przez ich liczbę. Gotowe.
Matematycy zapisują ją tak: xˉ (czytaj: “iks z kreseczką”). Brzmi groźnie? Spokojnie – to po prostu elegancki symbol na zwykłą średnią.
Masz trzy oceny z kolokwiów: 4, 5 i 3. Dodajesz: 4+5+3=12. Dzielisz przez 3 = wychodzi 4,0. To właśnie Twoja średnia arytmetyczna.
Kiedy średnia arytmetyczna ma sens w pracy magisterskiej?
✔️ Gdy chcesz sprawdzić “jaki jest przeciętny wynik” – np. średnia satysfakcja w ankiecie, średnia ilość godzin snu w tygodniu, średnia liczba lajków pod postami, średnia prędkość biegu na WF-ie albo średnia ocena wykładowcy.
✔️ Gdy masz liczby w tej samej skali – np. oceny w indeksie, punkty z testu wiedzy, złotówki wydane na kawę w miesiącu, liczbę kroków dziennie z aplikacji zdrowotnej.
✔️ Gdy dane są dość podobne i nie ma w nich “kosmitów” – np. wszyscy ankietowani mają wyniki zbliżone, więc średnia naprawdę coś mówi o całości.
Kiedy uważać na średnią arytmetyczną w pracy magisterskiej?
❌ Gdy masz skrajne wartości – np. jedna osoba zarabia 1000 zł, a inna 100 000 zł (średnia = “kosmos”), średnia wieku studentów wyniesie 25 lat, choć w grupie jest jeden 70-latek na studiach podyplomowych.
❌ Gdy dane są tylko uporządkowane, a nie mierzalne – np. odpowiedzi: “zdecydowanie się zgadzam”, “raczej się zgadzam”, “nie zgadzam się” (lepsza mediana lub moda), albo przy ocenianiu filmów: super, średni, słaby – nie policzysz z tego sensownej średniej.
❌ Gdy próbujesz uśredniać różne jednostki – np. 3 jabłka + 2 litry soku + 5 zł = średnia 3,3? Brzmi zabawnie, ale nie ma żadnej wartości badawczej.
Podsumowując, średnia arytmetyczna to prosty sposób, żeby w liczbach zobaczyć obraz całości – ale pamiętaj, że czasem może Cię trochę oszukać, jeśli nie spojrzysz na dane szerzej. 😉
Średnia arytmetyczna w pracy magisterskiej. Wzór + prosty przykład
Wzór ogólny na średnią arytmetyczną wygląda tak:
czyli: dodajesz wszystkie wartości x1,x2 ,…,xn i dzielisz przez ich liczbę n.
Krok po kroku (jak to policzyć):
- Zbierz liczby (np. wyniki ankiety, czasy, oceny).
- Policz sumę wszystkich wartości.
- Policz liczbę elementów n.
- Podziel sumę przez n.
- Nadaj jednostkę (jeśli są), zaokrąglij sensownie (np. do dwóch miejsc).
Żeby było jeszcze jaśniej, Weźmy sobie 3 liczby: 18, 22, 20.
- Suma: 18+22+20=60
- Liczebność: n=3
- Średnia: xˉ=60/3=20
Jak interpretować taki wynik?
- Jeśli to np. minuty oczekiwania, piszesz: „Średni czas oczekiwania wyniósł 20 minut.”
- Jeśli to skala 1–5, to 20 nie ma sensu – pamiętaj, średnia musi mieć tę samą skalę i jednostkę, co dane!
- W pracy naukowej raportuj elegancko: M = 20 (i zwykle dodaj SD albo SE w kolejnych sekcjach).
Inne średnie: kiedy arytmetyczna to za mało

Średnia ważona
Gdy Twoje obserwacje mają różną ważność (np. oceny z różną liczbą ECTS, ceny ważone liczbą sztuk w koszyku), zwykła średnia “spłaszcza” obraz. Średnia ważona przydziela każdej wartości wagę i bierze pod uwagę jej znaczenie. Różni się od arytmetycznej tym, że nie traktuje wszystkich elementów jednakowo.
Średnia geometryczna
Jeśli pracujesz na procentach, wzrostach, wskaźnikach mnożonych (np. roczna stopa zwrotu, średnie tempo wzrostu użytkowników rok do roku), to właściwy wybór. Zamiast dodawać i dzielić, geometryczna “uśrednia mnożenie” – daje sensowny “typowy” wzrost. Różni się od arytmetycznej tym, że lepiej opisuje procesy multiplikatywne i jest zwykle niższa od średniej arytmetycznej (chyba że wszystkie wartości są równe).
Uwaga! Średnia geometryczna wymaga wartości dodatnich.
Średnia harmoniczna
Idealna do uśredniania szybkości i stawek, czyli wielkości “na jednostkę” (km/h, zł/godz., szt./min), szczególnie gdy sumujesz odcinki o równej długości lub łączysz zmienne w postaci odwrotności. Różni się od arytmetycznej tym, że mocniej “kara” duże różnice i silnie reaguje na małe wartości (jedna bardzo niska prędkość/stawka mocno zaniży wynik).
Średnia kwadratowa (RMS)
Gdy liczy się moc sygnału, amplituda wahań albo chcesz uśrednić wartości dodatnie i ujemne tak, by nie znosiły się nawzajem (np. błędy dodatnie/ujemne, drgania), RMS robi robotę: najpierw podnosi do kwadratu, uśrednia, a na końcu pierwiastkuje. Różni się od arytmetycznej tym, że silniej podbija duże odchylenia (przez kwadrat), więc bywa od niej większa.
Po co liczy się średnią arytmetyczną w pracy magisterskiej?
Średnia liczy się po to, żeby z hałasu liczb zrobić jedno sensowne zdanie. W pracy dyplomowej to zdanie bywa kotwicą rozdziału „Wyniki”: zamiast surowych tabel możesz jasno napisać, że przeciętny poziom satysfakcji wyniósł M = 3,84/5, przeciętna liczba kroków to 7 900, a średni czas obsługi wniosku to 12 dni. Taki komunikat od razu ustawia punkt odniesienia na resztę analizy — wiadomo „jak jest” bez kombinowania.
Średnia pomaga też opowiedzieć historię różnic między grupami. Gdy porównasz M w grupie A i B, dostajesz natychmiastową odpowiedź „kto wypada lepiej i o ile”. Już sama różnica średnich (zanim wejdziesz w testy) pokazuje kierunek i skalę efektu: „uczestnicy programu mieli średnio o 0,58 punktu wyższą ocenę satysfakcji”. To język konkretny i intuicyjny, idealny do rozmowy z promotorem.
Kiedy pojawia się czas, średnia staje się termometrem trendu. Porównując średnie przed–po lub miesiąc do miesiąca, szybko odpowiadasz, czy coś rośnie, czy spada. Zdanie typu: „po wdrożeniu średni czas reakcji spadł z 420 ms do 360 ms” brzmi jak mini-opowieść z puentą. Jeśli chcesz wygładzić zygzaki — dorzucasz średnią ruchomą i masz czytelny trend.
Średnia świetnie nadaje się też do budowania wskaźników. Zamiast żonglować pięcioma pytaniami o satysfakcję, robisz z nich stabilny indeks (średnią z pozycji skali) i posługujesz się jedną liczbą w całej pracy. Zyskujesz prostotę i mniej kaprysów pojedynczych odpowiedzi.
Na koniec — średnia przyspiesza pisanie wniosków. Dwa–trzy zdania z liczbami brzmią profesjonalnie, a składają się z bardzo prostych obliczeń. Pamiętaj tylko o higienie: dane muszą być w tej samej skali, pilnuj wartości odstających, a obok średniej warto dodać SD/SE i — gdy rozkład jest skośny — wspomnieć medianę. Średnia jest świetna, ale nie zawsze jedyna.
Na jakich kierunkach studiów wykorzystać średnią arytmetyczną w pracy dyplomowej
Średnia arytmetyczna w pracy magisterskiej z pielęgniarstwa / Nauk o zdrowiu
Pomysły na tematy:
- „Ocena średniego natężenia bólu u pacjentów po zabiegach ortopedycznych – badanie porównawcze”.
- „Średnia arytmetyczna jakości snu (PSQI) u pielęgniarek pracujących zmianowo”.
- „Zmiana średniego poziomu glikemii przed i po edukacji diabetologicznej”.
- „Średnia satysfakcja pacjentów z teleporad w POZ”.
Co mierzyć? Skale Likerta 1–5 (satysfakcja, komunikacja), VAS bólu (0–10), czas oczekiwania (min), liczba kroków/dzień, wartości laboratoryjne (glukoza, ciśnienie).
Jak użyć średniej:
- Opis przeciętnego stanu: „M = 4,12/5”.
- Porównanie grup (np. dyżur dzienny vs nocny): różnica średnich.
- Przed–po interwencji: spadek średniej glikemii / bólu.
Zdanie do wyników:
„Średnie natężenie bólu po 48 h od zabiegu wyniosło M = 3,1/10 (SD = 1,4); w grupie z protokołem edukacyjnym było o 0,8 punktu niższe.”
Gdy masz skrajne czasy oczekiwania, pokaż także medianę.
Średnia arytmetyczna w pracy magisterskiej z administracji
Tematy:
- „Średnia ocena jakości e-usług urzędu X na podstawie ankiety mieszkańców”.
- „Średni czas obsługi sprawy a satysfakcja klienta – analiza korelacyjna”.
- „Przed i po: średnia liczba dni do wydania decyzji po wdrożeniu ePUAP”.
- „Średnia postrzegana dostępność informacji publicznej (1–5) w gminie Y”.
Co mierzyć? skale 1–5 (jakość, dostępność), czas w dniach, liczba wizyt/telefonów, koszt sprawy.
Jak użyć średniej:
- Benchmark gmin/działów: „u nas M = 3,7, w powiecie M = 3,4”.
- Monitoring trendu miesiąc do miesiąca (średnia ruchoma, jeśli chcesz wygładzić).
Zdanie do wyników:
„Po wprowadzeniu formularzy online średni czas obsługi spadł z 13,6 do 9,2 dnia (−32%).”
Jeśli rozkład czasu jest mocno skośny, porównaj M i medianę.
Średnia arytmetyczna w pracy magisterskiej z zarządzania / HR
Tematy:
- „Średnie zaangażowanie pracowników (UWES) a staż pracy – badanie przekrojowe”.
- „Średni poziom stresu w pracy zmianowej – analiza branżowa”.
- „Średnia satysfakcja z wynagrodzenia vs średnia intencja odejścia (porównanie działów)”.
- „Średnia liczba szkoleń na pracownika a samoocena kompetencji”.
Co mierzy? Skale Likerta (zaangażowanie, stres, satysfakcja), liczba szkoleń, rotacja (tak/nie → lepiej uśredniać wskaźnik procentowy w czasie).
Jak użyć średniej:
- Indeks z kilku pytań (średnia pozycji skali).
- Różnice między działami – czytelne i lubiane przez kadrę.
- Przed–po wdrożeniu programu wellbeing.
Zdanie do wyników:
„W dziale A średnie zaangażowanie wyniosło M = 4,3, a w dziale B M = 3,8; różnica 0,5 pkt.”
Dla rotacji używaj średniej miesięcznych wskaźników (a nie ‘średniej z tak/nie’).
Średnia arytmetyczna w pracy magisterskiej z informatyki
Tematy:
- „Średni czas wykonania zadania w aplikacji mobilnej po zmianie nawigacji”.
- „Średnia ocena użyteczności (SUS) nowego interfejsu vs poprzedni”.
- „Średnia liczba kliknięć do celu (C/D) w teście scenariuszowym”.
- „Średni czas ładowania strony przed i po optymalizacji (Core Web Vitals)”.
Co mierzyć? czas (ms/s), liczba kliknięć, SUS (0–100), NPS (−100–100), błędy na zadanie.
Jak użyć średniej:
- Średnie czasy jako główny KPI.
- Porównanie wariantów A/B (różnica średnich).
- Trend dzienny/tygodniowy – średnie ruchome.
Zdanie do wyników:
„Po zmianie nawigacji średni czas ukończenia zadania skrócił się z 42 s do 31 s (−26%).”
Przy czasach dorzuć SD – pokaże rozrzut (użyteczne w UX).
Średnia arytmetyczna w pracy magisterskiej z pedagogiki / Edukacji
Tematy:
- „Średni wynik testu kompetencji po wdrożeniu metod aktywizujących”.
- „Średnia frekwencja miesięczna a poczucie przynależności do klasy (1–5)”.
- „Średnia ocena skuteczności zajęć arteterapeutycznych (1–5)”.
- „Średnia liczba godzin nauki własnej a wynik egzaminu”.
Co mierzyć? wyniki testów (pkt %), frekwencja (%), skale samopoczucia (1–5), czas nauki (h/tydz.).
Jak użyć średniej:
- Efekt edukacyjny (przed–po).
- Porównania klas/technik nauczania.
- Indeksy (średnia z kilku pytań motywacyjnych).
Zdanie do wyników:
„Po cyklu warsztatów średni wynik testu wzrósł z 62% do 74%.”
Oceny szkolne to skala porządkowa – średnia jest ok umownie, uzupełnij medianą.
Średnia arytmetyczna w pracy magisterskiej z bezpieczeństwa wewnętrznego / Kryminologii
Tematy:
- „Średni czas reakcji służb na zdarzenia w powiecie X – analiza zmian rocznych”.
- „Średnia ocena poczucia bezpieczeństwa mieszkańców (1–5) vs liczba interwencji”.
- „Średnia liczba wykroczeń w strefach patrolowych – porównanie rejonów”.
- „Średnia skuteczność profilaktyki (kampanie) w zmianie wiedzy obywateli”.
Co mierzyć? czasy (min), liczba interwencji/mies., ocena bezpieczeństwa (1–5), liczba zdarzeń na 1000 mieszkańców.
Jak użyć średniej:
- Benchmark dzielnic/rejonów.
- Trend (spadek średniej liczby zdarzeń po działaniach prewencyjnych).
- Przed–po kampanii.
Zdanie do wyników:
„Po wprowadzeniu patroli prewencyjnych średnia liczba kradzieży kieszonkowych spadła z 18 do 11 mies./rejon.”
Wskaźniki zdarzeń bywają sezonowe — pokaż średnie miesięczne z kilku lat.
Średnia arytmetyczna w pracy magisterskiej z Fizjoterapii
Tematy:
- „Średnia prędkość biegu na 5 km a tętno spoczynkowe – korelacja”.
- „Średnie RPE (zmęczenie) po wprowadzeniu interwałów HIIT”.
- „Średnia liczba powtórzeń do upadku mięśniowego w planie A vs B”.
- „Średni zakres ruchu (ROM) po 6 tygodniach fizjoterapii”.
Co mierzyć? czasy, prędkości, tętno, RPE (1–10), ROM (°), liczba powtórzeń.
Jak użyć średniej:
- Przed–po treningu/interwencji.
- Porównanie planów treningowych.
- Średnie tygodniowe do kontroli obciążeń.
Zdanie do wyników:
„Po 6 tygodniach interwencji średni ROM zgięcia barku wzrósł z 132° do 151°.”
Tip: wartości skrajnie wysokie (talenty 😉) mogą zawyżać M — rzuć okiem na medianę.
Dane do średniej arytmetycznej. Jak je przygotować, żeby wynik miał sens
Żeby średnia arytmetyczna mówiła prawdę, musisz zadbać o jakość danych. To jak z ciastem: nawet najlepszy przepis nic nie da, jeśli składniki są byle jakie. Poniżej masz prosto wyjaśnione, kiedy wolno liczyć średnią, co zrobić z brakami i zerami oraz jak ogarnąć “kosmitów” (wartości odstające) – wszystko “po ludzku”.
1) Skale pomiarowe – kiedy średnia jest OK (i kiedy nie)
- Skala nominalna – to etykiety/nazwy: np. płeć, kierunek studiów, marka telefonu.
Średnia- nie liczymy. Tu pytasz o najczęstszy wybór (dominanta/moda), nie o przeciętną.
- Skala porządkowa (ordinalna) – mamy kolejność, ale nie wiemy, “o ile więcej”: np. skala Likerta 1–5 (“zdecydowanie się nie zgadzam” → “zdecydowanie się zgadzam”).
Średnia- ostrożnie. W pracach studenckich często umownie liczy się średnią, ale obowiązkowo dorzuć medianę (wartość środkową) i modę (najczęstszą odpowiedź), bo to lepiej oddaje takie dane.
- Skala przedziałowa (intervalowa) – różnice mają sens, ale zero jest umowne (np. °C).
Średnia- tak, można liczyć.
- Skala ilorazowa (stosunkowa) – różnice i prawdziwe zero (np. kg, zł, minuty, liczba kroków).
Średnia- tak, to idealne miejsce dla średniej.
Jeśli Twoje liczby to wyniki/sumy/czasy/kwoty – licz średnią. Jeśli to etykiety – nie. Jeśli to kolejność/stopień zgody – możesz, ale koniecznie pokaż też medianę.
2) Braki danych vs zera – to NIE jest to samo
- Brak danych = ktoś nie odpowiedział / puste pole / nie dotyczy.
To nie jest zero. Jeśli potraktujesz brak jak 0, zaniżysz średnią (np. średnia ocen, średnia liczba godzin snu).
Co robić?- Albo pomijasz braki przy liczeniu średniej (najczęściej),
- albo opisujesz, ile ich było (np. “braki 6,8%”).
- Jeśli “nie dotyczy” – trzymaj to w osobnej kategorii, nie mieszaj z liczbami.
- Zero (0) = prawdziwa wartość.
Np. 0 min czekania, 0 zł kosztu, 0 kroków danego dnia. Zero wchodzi do średniej, bo to realny wynik.
Krótko: puste ≠ 0. Puste wyłącz, zero wlicz.
3) Wartości odstające (“kosmici”) – jak je rozpoznać i co z nimi zrobić
Wartość odstająca to liczba, która mocno odstaje od reszty (np. czasy 5–12 min i nagle 120 min). Taki “kosmita” potrafi wywrócić średnią.
Proste sposoby kontroli:
- Zdrowy rozsądek: czy to w ogóle możliwe? 400 lat życia? 800 kg masy? Jeśli błąd wpisu – popraw albo usuń z uzasadnieniem.
- Szybki próg: przyjrzyj się wartościom 3× SD od średniej, gdzie SD to odchylenie standardowe (ang. standard deviation) – miara “rozrzutu” danych. Jeśli coś leży bardzo daleko, oznacz i sprawdź.
- IQR/rozstęp międzykwartylowy (ang. interquartile range): to różnica między kwartylem 75% a 25%. Gdy coś wypada poniżej Q1 − 1,5×IQR albo powyżej Q3 + 1,5×IQR, jest kandydatem na “odstające”. (Nie musisz liczyć ręcznie — ważne, żebyś wiedział/a, że sprawdziłeś/aś).
Co dalej?
- Jeśli to błąd – koryguj/usuń (zapisz to w metodologii).
- Jeśli to rzeczywisty wynik, ale rzadki – zostaw, ale w analizie pokaż też medianę i/lub zrób porównanie bez tych przypadków jako analizę czułości (napisz, czy wnioski się zmieniły).
4) Zanim policzysz średnią – mini check-lista „higieny danych”
- Ta sama skala i jednostki- jeśli łączysz minuty i godziny – przelicz na jedno (np. wszystko w minutach).
- Ten sam kierunek skali- na skali zgody 1 = mniej, 5 = więcej. Upewnij się, że nigdzie nie jest odwrotnie.
- Braki ≠ zera- puste pola wyłącz, zera zostaw.
- Grupy o różnej wielkości- gdy łączysz procenty/średnie z różnych grup, użyj średniej ważonej (większa grupa ma większą wagę).
- Outliery- rzuć okiem na skrajności, sprawdź błędy i rozważ pokazanie median(y) obok średniej.
- Opisuj n- zawsze podaj liczność próby (n) – średnia bez n to półprawda.
- Rozrzut- razem ze średnią dorzuć SD (odchylenie standardowe) albo SE (standard error = błąd standardowy średniej, czyli SD/√n). To jedno zdanie, a robi wrażenie.
- Spójność próby- nie mieszaj danych, które nie powinny być razem (np. dzieci i dorośli w jednym “worku”, jeśli różnice są oczywiste i badanie tego nie zakłada).
5) Jak to ładnie opisać w pracy (jedno zdanie do wklejenia)
„Przed obliczeniem średnich przeprowadzono kontrolę jakości danych: ujednolicono jednostki, wyłączono braki odpowiedzi (puste pola nie były traktowane jako 0), a wartości odstające zweryfikowano i – w przypadku błędów wpisu – usunięto. W wynikach raportowano średnią (M) wraz z odchyleniem standardowym (SD) oraz liczebnością (n); dla zmiennych na skali porządkowej dodatkowo podano medianę.”
Jak obliczyć średnią arytmetyczną w Excelu (krok po kroku)?
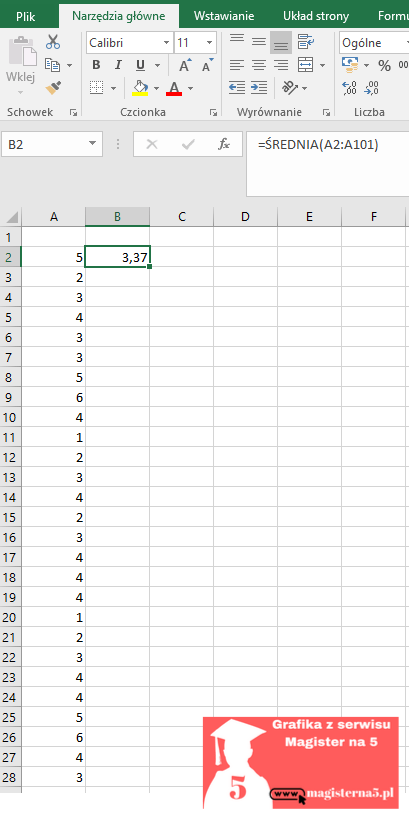
A teraz usiądźmy „ramię w ramię” i zróbmy to po ludzku. Otwierasz Excela, w jednej kolumnie wklejasz swoje liczby (zostaw nagłówek w A1, dane od A2 w dół). Teraz w wolnej komórce wpisujesz formułę =ŚREDNIA(A2:A101) i wciskasz Enter. To wszystko.
Jeśli chcesz elegancko zabezpieczyć się przed brzydkim błędem, który pojawia się, gdy w zakresie nie ma żadnej liczby, zamień formułę na =JEŻELI.BŁĄD(ŚREDNIA(A2:A101);”—”) — wtedy zamiast błędu zobaczysz kreskę.
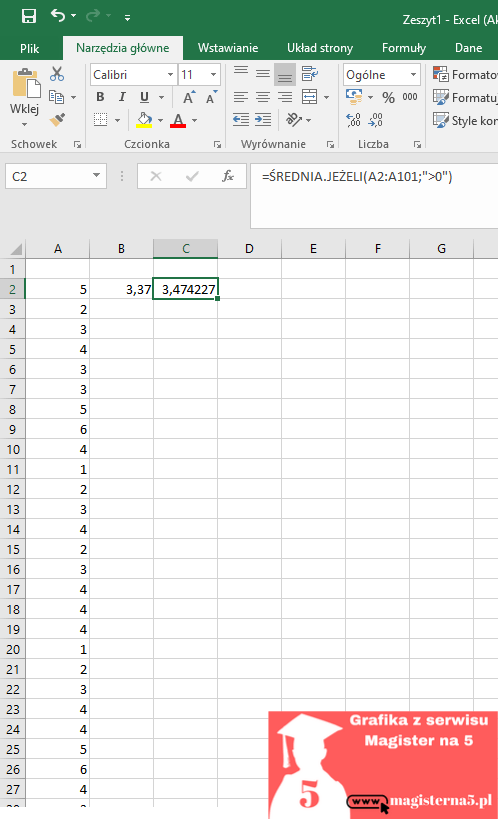
A gdy zależy Ci, by pominąć zera (bo np. zero oznacza „nie mierzono”), użyj wersji =ŚREDNIA.JEŻELI(A2:A101;”>0″).
Zaokrąglenie? Albo ustaw format liczbowy komórki, albo na szybko dopisz ZAOKR(…;2) i masz dwie cyfry po przecinku.
Najczęstsze potknięcia
Pierwsze: puste komórki to nie zera. Puste Excel po prostu ignoruje, zera natomiast liczy i zaniża wynik — dlatego, jeśli „0” to u Ciebie „brak”, skorzystaj z tej wersji z ŚREDNIA.JEŻELI.
Drugie: liczby zapisane jako tekst. Poznasz je po tym, że są wyrównane do lewej i często mają zielony trójkącik. Kliknij ostrzeżenie „Konwertuj na liczbę” albo użyj „Dane → Tekst jako kolumny → Zakończ”, ewentualnie pomocniczo =WARTOŚĆ(A2).
Trzecie: zły zakres — niech formuła nie obejmuje nagłówka; zaczynaj od A2, nie od A1. I jeszcze drobiazg: w polskim Excelu używamy przecinka jako separatora dziesiętnego (3,14), a nazwy funkcji są po polsku (czyli ŚREDNIA, nie AVERAGE). Jeśli filtrujesz dane i chcesz średnią tylko z widocznych wierszy, zamiast zwykłej ŚREDNIA wstaw =AGREGUJ(1;5;A2:A101) — wtedy ukryte wiersze nie będą brane do rachunku.
To naprawdę wszystko. Dajesz dane w kolumnę, liczysz ŚREDNIA(…), a potem — w zależności od potrzeb — dodajesz małe „wygładzacze”: pomijanie zer, zaokrąglenie, ochrona przed błędem. Reszta to już czysta interpretacja w rozdziale „Wyniki”.
Jak opisać i zinterpretować średnią arytmetyczną w pracy?
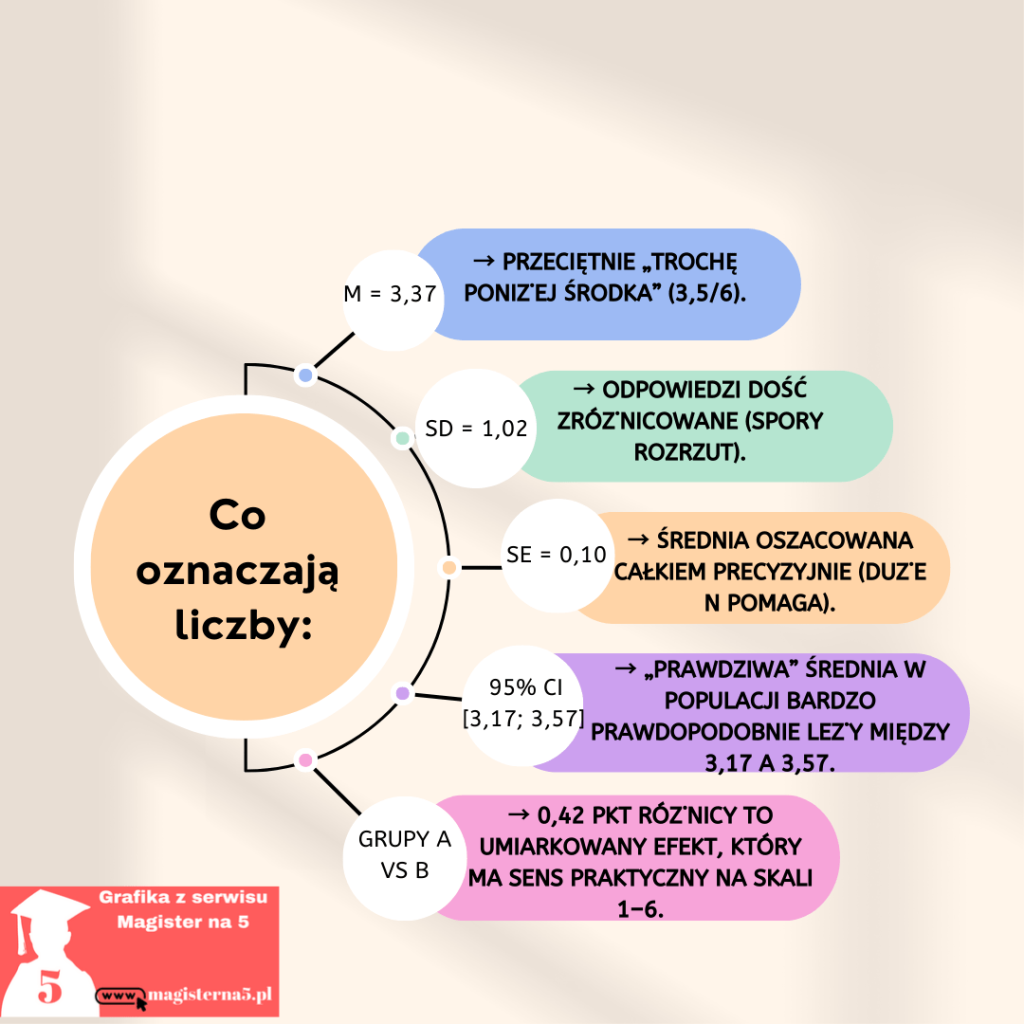
„Do opisu tendencji centralnej zastosowano średnią arytmetyczną (M) wraz z odchyleniem standardowym (SD), błędem standardowym średniej (SE) oraz 95% przedziałem ufności (CI) dla skali 1–6.”
Wyniki (z konkretnymi liczbami):
„Średnia wartość badanej cechy wyniosła M = 3,37 przy n = 100. Zróżnicowanie wyników opisuje SD = 1,02, a precyzję estymacji średniej SE = SD/√n = 1,02/10 = 0,10. 95% CI: [3,17; 3,57].”
Interpretacja (po ludzku, na skali 1–6):
„Wynik 3,37 leży nieco poniżej środka skali (środek = 3,5), co sugeruje umiarkowany poziom z lekkim przechyłem w dół. Po przeskalowaniu względem zakresu 1–6 odpowiada to ok. 47,4% całej skali [(3,37−1)/(6−1)]⋅100%”
Porównanie grup (jeśli masz dwie grupy – przykład do wklejenia):
„W grupie A uzyskano Mₐ = 3,58 (SD = 0,96; n = 52), a w grupie B Mᵦ = 3,16 (SD = 1,08; n = 48); różnica średnich = 0,42 pkt. Szacunkowy 95% CI różnicy: [0,02; 0,82], co wskazuje na wyraźną, choć umiarkowaną przewagę grupy A.”
Dyskusja (jedno zdanie finału):
„Uzyskana średnia wskazuje na umiarkowany, lekko obniżony poziom; biorąc pod uwagę SD = 1,02, SE = 0,10 i 95% CI [3,17; 3,57], wnioski są stosunkowo stabilne, choć dla pełniejszego obrazu warto równolegle podać medianę (np. Med = 3,0; IQR = 3–4) przy ewentualnej skośności rozkładu.”
Mini-case’y średniej arytmetycznej do różnych kierunków studiów
Zdrowie (nasilenie bólu, 0–10)
Po 7 dniach terapii średnie natężenie bólu spadło z 6,2 do 3,9. W praktyce: pacjenci deklarują odczuwalnie mniejszy ból niż na początku.
Administracja (jakość e-usług, skala 1–5)
Mieszkańcy ocenili jakość e-usług na średnio 3,8/5. To znaczy: ogólnie jest „na plus”, ale wciąż jest miejsce na poprawę.
HR (stres w pracy, skala 1–5)
W dziale A średni poziom stresu wyniósł 3,2, a w dziale B 2,7. Dział B raportuje zatem nieco niższy stres na co dzień.
IT (czas ładowania strony, sekundy)
Po optymalizacji średni czas ładowania skrócił się z 3,4 s do 2,5 s. Użytkownik szybciej widzi treść — to realna poprawa.
Edukacja (wynik testu, %)
Średni wynik testu końcowego to 74%, podczas gdy na starcie było 62%. Studenci podciągnęli się średnio o 12 p.p. w trakcie kursu.
Najczęstsze błędy związane ze średnią arytmetyczną i jak ich uniknąć
Outliery (wartości odstające)
Jeden „kosmita” potrafi wykrzywić średnią jak plastelinę — np. czasy 5–12 min i nagle 120 min. Najpierw sprawdź, czy to błąd wpisu (literówka, zła jednostka). Jeśli to realny wynik, pokaż też medianę i zrób krótką analizę czułości (porównaj średnią z i bez tej obserwacji). W pracy jedno zdanie wyjaśnienia wystarczy.
Skale porządkowe (Likert 1–5, „zgadzam się” itd.).
Średnia tu bywa „umowna”, bo nie wiemy, o ile „raczej się zgadzam” jest większe od „ani tak, ani nie”. Możesz podać średnią (promotorzy często tego oczekują), ale koniecznie dodaj medianę i/lub modę oraz krótko napisz, że skala ma charakter porządkowy. Jeśli masz pozycje „odwrócone” (gdzie 1 znaczy „więcej”), przekoduj je przed liczeniem.
Pomyłki w wagach (średnia ważona).
Najczęściej myli się co jest wagą i w jakiej skali ją wpisać. Wagi to „ile waży” obserwacja: ECTS, liczba sztuk, liczebność grupy. Wpisuj liczby, nie procenty z „%” (albo używaj ułamków dziesiętnych). Nie ma potrzeby „ręcznie normalizować” wag — dzielenie przez sumę wag robi to za Ciebie. Zawsze sprawdź, czy sum(wagi) > 0.
Mylenie SD z SE.
SD (odchylenie standardowe) opisuje rozrzut danych w próbie („jak różnimy się między sobą”). SE (błąd standardowy średniej) opisuje precyzję średniej jako estymatora („na ile pewnie znamy M”). Do opisu zmienności grupy podawaj SD, do przedziałów ufności dla średniej używaj SE (SE = SD/√n). Nie zamieniaj ich miejscami.
„Średnia z procentów” bez ważenia.
Dwie klasy: w jednej zdawalność 50% z 10 osób, w drugiej 50% ze 100 osób — prosta średnia procentów da 50%, ale to akurat przypadek szczęśliwy. Gdy odsetki różnią się, uśredniaj ważoną: zsumuj liczbę zdarzeń (np. zdanych) i liczbę wszystkich przypadków, a potem podziel (czyli licz globalny odsetek, nie „średnią z odsetków”). To samo dotyczy stawek, współczynników, frekwencji.
Wady i zalety średniej arytmetycznej + kiedy wybrać inną miarę
Średnia arytmetyczna to taki statystyczny „bread & butter”. Szybka, prosta, każdy ją kojarzy. Ale, jak każdy skrót – ma swoje plusy i minusy.
Zalety (czyli za co ją kochamy)
- Prosta jak drut – dodajesz, dzielisz, gotowe.
- Czytelna – jedno liczko, które każdy rozumie („przeciętnie mamy 3,8/5”).
- Wspólna waluta porównań – łatwo zestawić grupy (A vs B) albo „przed–po”.
Wady (czyli gdzie potrafi namieszać)
- Wrażliwa na kosmitów (wartości odstające): jedna pensja 100 tys. zł w grupie zawyża „przeciętne zarobki” jak szalona.
- Nie lubi skal porządkowych (typu „zdecydowanie się zgadzam” → „zdecydowanie się nie zgadzam”) – traktuje je jak odległości, a to nie do końca prawda.
- Bywa myląca przy rozkładach skośnych – średnia idzie w stronę ogona, a „typowy” przypadek wcale tak nie wygląda.
Kiedy wybrać inną miarę (i jaką)?
- Masz odklejone skrajności / skośny rozkład?
Bierz medianę (wartość środkowa). Jest odporna na kosmitów i często lepiej opisuje „typowy” przypadek niż średnia. - Dane są kategoryczne / chcesz „najczęściej wybieraną” odpowiedź?
To robota dla dominanty (mody) – wskazuje, co występuje najczęściej. - Różne wagi/znaczenia obserwacji (ECTS, liczba sztuk, wielkości grup)?
Średnia ważona – każda wartość wnosi tyle, ile „waży”. Prościej i uczciwiej. - Pracujesz na wzrostach procentowych, stopach zwrotu, mnożeniu efektów?
Średnia geometryczna – „uśrednia mnożenie”, sensowna dla dynamik i procentów. - Uśredniasz prędkości, stawki „na jednostkę”, tempo na odcinkach o równej długości?
Średnia harmoniczna – lepiej traktuje „na jednostkę” i mocniej reaguje na niskie wartości. - Masz sporo śmieciowych skrajności, ale chcesz jednak „średniej”?
Średnia obcięta (trimmed mean) – liczysz średnią po ucięciu skrajnych 5–10% wartości z dołu i z góry. Kompromis między średnią a medianą. - Serie czasowe i trend w czasie?
Średnia ruchoma – wygładza zygzaki, pokazuje kierunek zmian.
Jeśli masz wątpliwość, policz M + medianę i rzuć okiem, jak się różnią. Duża różnica = sygnał: Twoje dane mogą być skośne lub z kosmitami – wtedy średnia nie jest jedyną królową balu.
Średnia arytmetyczna w pracy magisterskiej podsumowanie
Jeśli miał(a)byś zapamiętać z tego artykułu tylko jedną rzecz, niech to będzie ta: średnia arytmetyczna to najszybszy sposób na ogarnięcie liczb i zamianę ich w czytelny wniosek.
W pracy dyplomowej robi robotę jako kotwica wyników (masz jedno, zrozumiałe „jak jest”), fundament porównań grup i prosty termometr trendów. Liczysz ją w minutę, a potem dorzucasz M + SD/SE + 95% CI, pilnujesz odstających i — kiedy trzeba — sięgasz po medianę lub średnią ważoną. Prosto, uczciwie, profesjonalnie.
Masz wszystko, żeby Twoje „Wyniki” były klarowne, rzeczowe i przekonujące. A teraz — do dzieła. Niech moc będzie z Tobą.
Trochę już wiem o średniej arytmetycznej w pracy magisterskiej. Teraz chcę poznać proces pisania
Naucz się pisać pracę w godzinę. Sprawdź e-book.
Jak napisać pracę w tydzień?
E-book- Jak napisać pracę dyplomową w tydzień? Pobieram teraz>>
Pobieram teraz>>
Dlaczego ten e-book może Ci bardzo pomóc?
- 85 stron samych konkretów- materiał do błyskawicznego wykorzystania.
- Pokaże Ci jak zacząć już za 5 minut. Bez zastanawiania się i marnowania czasu.
- Pokonasz perfekcjonizm i przestaniesz okładać na później.
- Dowiesz się jak pisać pracę 10 razy szybciej, stosując metodę Magistra na 5.
- Uprościliśmy temat, jak tylko się dało. Zrozumiesz, nawet jak nigdy nie pisałeś żadnej pracy.
- Przeczytasz w godzinę. Już nie musisz marnować czasu na dojazdy na uczelnie i seminaria.
- Dostęp w 30 sekund. Materiał dostaniesz w prosto na maila.
- Dostajesz dostęp do wszystkich aktualizacji. Ten produkt to mój absolutny priorytet. Cały czas go ulepszam i dodaje nowe materiały.
- Dużo przykładów. Nie wymyślasz nic od nowa.
- Schematy i wzory działania. Prowadzimy Cię jak po sznurku.
- Dodatkowe ćwiczenia. Zaczniesz działać już na 5 minut.
- Za cenę 4 kaw w Żabce.
Potrzebujesz pomocy z najtrudniejszą częścią swojej pracy?
Metodologia, rozdział badawczy, analiza statystyczna. Błyskawiczna pomoc>>
--
Zobacz opinie:
Zobacz, jakie materiały mogę Ci jeszcze zaproponować.
–>Sklep Magistra na 5
Jeżeli potrzebujesz pomocy, po prostu napisz.
–> Wyślij pytanie




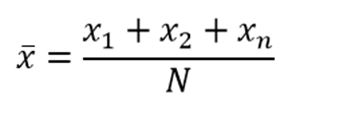




 Pobieram teraz>>
Pobieram teraz>>




